题目内容
16.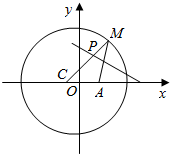 已知圆C:(x+1)2+y2=25,定点A(1,0),M为圆上的一个动点,连接MA,作MA的垂直平分线交半径MC于P,当M点在圆周上运动时,点P的轨迹方程为$\frac{{x}^{2}}{\frac{25}{4}}+\frac{{y}^{2}}{\frac{21}{4}}=1$.
已知圆C:(x+1)2+y2=25,定点A(1,0),M为圆上的一个动点,连接MA,作MA的垂直平分线交半径MC于P,当M点在圆周上运动时,点P的轨迹方程为$\frac{{x}^{2}}{\frac{25}{4}}+\frac{{y}^{2}}{\frac{21}{4}}=1$.
分析 根据圆C的标准方程得到点C(-1,0),半径R=5.再由线段中垂线定理,可化简出PC+PA=5,从而得出点P的轨迹C是以C、A为焦点,2a=5的椭圆.最后根据椭圆的基本概念,即可得出点P的轨迹对应的椭圆的标准方程.
解答 解:∵圆C方程为:(x+1)2+y2=25,
∴点C(-1,0),半径R=5,
∵MA的垂直平分线交半径MC于P,
∴PM=PA,可得PC+PA=CM.
∵点M是圆C上的动点,∴CM长为圆C的半径5,
∴动点P满足PC+PA=5,点P的轨迹是以C、A为焦点,2a=5的椭圆.
可得a2=$\frac{25}{4}$,c=1,b2=a2-c2=$\frac{21}{4}$,
∴轨迹的方程为$\frac{{x}^{2}}{\frac{25}{4}}+\frac{{y}^{2}}{\frac{21}{4}}=1$.
故答案为:$\frac{{x}^{2}}{\frac{25}{4}}+\frac{{y}^{2}}{\frac{21}{4}}=1$.
点评 本题借助一个动点的轨迹,得到椭圆的第一定义,进而求出其轨迹方程.着重考查了线段的垂直平分线定理和椭圆的基本概念等知识点,属于基础题.

练习册系列答案
相关题目
6.已知A={0,1},B={-1,0,1},则从B到A的不同映射的有( )
| A. | 8个 | B. | 9个 | C. | 5个 | D. | 6个 |
8. 下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:
下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:
(1)请在给出的坐标系中画出上表数据的散点图;
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程$\stackrel{∧}{y}=\stackrel{∧}{b}x+\stackrel{∧}{a}$;
(3)估计使用年限为10年时,维修费用为多少?
(参考数值:$\sum_{i=1}^{5}{x}_{i}{y}_{i}=112.3$ $\sum_{i=1}^{5}{{x}_{i}}^{2}=80$)
(参考公式:$\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$;$\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}$;)
 下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:
下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程$\stackrel{∧}{y}=\stackrel{∧}{b}x+\stackrel{∧}{a}$;
(3)估计使用年限为10年时,维修费用为多少?
(参考数值:$\sum_{i=1}^{5}{x}_{i}{y}_{i}=112.3$ $\sum_{i=1}^{5}{{x}_{i}}^{2}=80$)
(参考公式:$\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$;$\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}$;)
5.已知集合A={x|y=lgx},B={y|y=2x},则( )
| A. | A⊆B | B. | A∩B=∅ | C. | A=B | D. | A∪B=R |