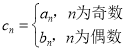题目内容
【题目】二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格y(单位:万元/辆)进行整理,得到如下数据:
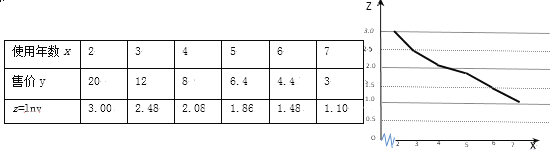
如图是z关于x的折线图:
(1)由折线图可以看出,可以用线性回归模型拟合z和x的关系,请用相关系数r加以说明(注:若相关系数︱r︱![]() 0.75,则认为两个变量相关程度较强);
0.75,则认为两个变量相关程度较强);
(2)求y关于x的回归方程并预测某辆A型号二手车当使用年数为9年时售价约为多少?(![]() 小数点后面保留两位有效数字);
小数点后面保留两位有效数字);
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号的二手车时车辆的使用年限不得超过多少年?
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
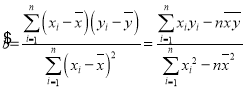 ,
,
参考数据: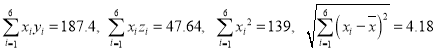
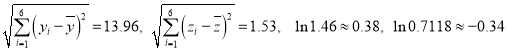
【答案】(1)![]() 与
与![]() 的线性相关程度很高;(2)
的线性相关程度很高;(2)![]() ,1.46万元;(3)11年.
,1.46万元;(3)11年.
【解析】
(1)由表格数据,求出![]() ,再把参考数据代入公式,求出相关系数
,再把参考数据代入公式,求出相关系数![]() ,即得答案;
,即得答案;
(2)根据参考公式求出![]() 关于
关于![]() 的线性回归方程,又
的线性回归方程,又![]() ,可求出y关于x的回归方程
,可求出y关于x的回归方程![]() ,把
,把![]() 代入,求出答案;
代入,求出答案;
(3)令![]() ,解不等式即得.
,解不等式即得.
(1)由题意,知![]() ,
,
![]() ,
,
又![]() ,
, 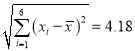 ,
, 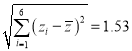 ,
,
∴ ,
,
∴![]() 与
与![]() 的相关系数大约为-0.99,说明
的相关系数大约为-0.99,说明![]() 与
与![]() 的线性相关程度很高
的线性相关程度很高
(2) 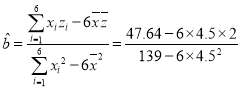
![]() ,
,
∴![]() ,
,
∴![]() 与
与![]() 的线性回归方程是
的线性回归方程是![]() ,
,
又![]() ,∴
,∴![]() 关于
关于![]() 的回归方程是
的回归方程是![]() .
.
令![]() ,
,
得![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
即预测某辆![]() 型号二手车当使用年数为9年时售价约为1.46万元
型号二手车当使用年数为9年时售价约为1.46万元
(3)当![]() ,
,
即![]() 时,
时,
则有![]() , 解得
, 解得![]() ,
,
因此,预测在收购该型号二手车时车辆的使用年数不得超过11年

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】端午节(每年农历五月初五),是中国传统节日,有吃粽子的习俗.某超市在端午节这一天,每售出![]() kg粽子获利润
kg粽子获利润![]() 元,未售出的粽子每
元,未售出的粽子每![]() kg亏损
kg亏损![]() 元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了
元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了![]() kg粽子.以
kg粽子.以![]() (单位:kg,
(单位:kg,![]() )表示今年的市场需求量,
)表示今年的市场需求量,![]() (单位:元)表示今年的利润.
(单位:元)表示今年的利润.
市场需求量(kg) |
|
|
|
|
|
频率 | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据频率分布表估计今年利润![]() 不少于
不少于![]() 元的概率.
元的概率.
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为![]() .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么![]() 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A.![]() 倍B.
倍B.![]() 倍C.
倍C.![]() 倍D.
倍D.![]() 倍
倍