题目内容
12.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,过F2作平行于C的渐近线的直线交C于点P.若PF1⊥PF2,则C的离心率为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 设P(x,y),通过联立直线PF2的方程、直线PF1的方程及双曲线方程,计算即可.
解答 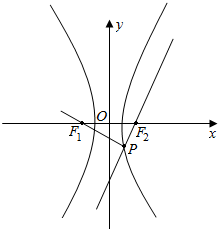 解:如图,设P(x,y),
解:如图,设P(x,y),
根据题意可得F1(-c,0)、F2(c,0),
双曲线的渐近线为:y=$\frac{b}{a}$x,
直线PF2的方程为:y=$\frac{b}{a}$(x-c),①
直线PF1的方程为:y=-$\frac{a}{b}$(x+c),②
又点P(x,y)在双曲线上,∴$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,③
联立①③,可得x=$\frac{{a}^{2}+{c}^{2}}{2c}$,
联立①②,可得x=$\frac{{b}^{2}-{a}^{2}}{{a}^{2}+{b}^{2}}$•c=$\frac{{b}^{2}-{a}^{2}}{c}$,
∴$\frac{{a}^{2}+{c}^{2}}{2c}$=$\frac{{b}^{2}-{a}^{2}}{c}$,
∴a2+a2+b2=2b2-2a2,
∴b2=4a2,
∴e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{\frac{5{a}^{2}}{{a}^{2}}}$=$\sqrt{5}$,
故选:D.
点评 本题考查求双曲线的离心率,考查计算能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
20. 如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )
如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )
 如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )
如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | 8 |
17.某射击手射击一次命中的概率是0.7,连续两次均射中的概率是0.4,已知某次射中,则随后一次射中的概率是( )
| A. | $\frac{7}{10}$ | B. | $\frac{6}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{2}{5}$ |
4.下列函数中,既是奇函数,又在(-∞,+∞)上为增函数的是( )
| A. | y=3x | B. | y=$\frac{1}{x}$ | C. | y=x3 | D. | y=tanx |
1.若集合A={x|-x2+7x-10<0}与B={x||2x+1|<3},则下列选项中正确的是( )
| A. | A⊆B | B. | A?B | C. | B?A | D. | A=B |
 如图,多面体ABCD-A1E中,底面ABCD为正方形,AA1⊥平面ABCD,CE⊥平面ABCD,AA1=2AB=4,且CE=λAA1,A1C⊥平面BED.
如图,多面体ABCD-A1E中,底面ABCD为正方形,AA1⊥平面ABCD,CE⊥平面ABCD,AA1=2AB=4,且CE=λAA1,A1C⊥平面BED.