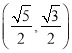题目内容
【题目】椭圆![]() +
+![]() =1的左、右焦点分别为F1,F2,一条直线
=1的左、右焦点分别为F1,F2,一条直线![]() 经过点F1与椭圆交于A,B两点.
经过点F1与椭圆交于A,B两点.
(1)求△ABF2的周长;
(2)若![]() 的倾斜角为
的倾斜角为![]() ,求弦长|AB|.
,求弦长|AB|.
【答案】(1)8(2)![]()
【解析】试题分析:解决椭圆问题要注意“勿忘定义”,根据椭圆的定义,把三角形周长看成点A到两焦点的距离和及点B到两焦点距离和,求椭圆的弦长利用弦长公式,一般设而不求,把直线方程和椭圆方程联立方程组,借助根与系数的关系,利用![]() 和
和![]() 求弦长.
求弦长.
试题解析:
(1)椭圆![]() ,a=2,b=
,a=2,b=![]() ,c=1,
,c=1,
由椭圆的定义,得丨AF1丨+丨AF2丨=2a=4,丨BF1丨+丨BF2丨=2a=4,
又丨AF1丨+丨BF1丨=丨AB丨,
∴△ABF2的周长为![]()
∴故△ABF2点周长为8;
(2)由(1)可知,得F1(﹣1,0),
∵AB的倾斜角为![]() ,则AB斜率为1,A(x1,y1),B(x2,y2),
,则AB斜率为1,A(x1,y1),B(x2,y2),
故直线AB的方程为y=x+1. 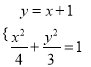 ,整理得:7y2﹣6y﹣9=0,
,整理得:7y2﹣6y﹣9=0,
由韦达定理可知:y1+y2=![]() ,y1y2=﹣
,y1y2=﹣![]() ,
,
则由弦长公式丨AB丨=![]()
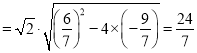 ,
,
弦长|AB|=![]() .
.

练习册系列答案
相关题目