题目内容
已知锐角α、β满足sinα=
，cosβ=
，则cos（α-β）的值是 ．
| ||
| 5 |
3
| ||
| 10 |
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：由同角三角函数的基本关系可得cosα和sinβ，而cos（α-β）=cosαcosβ+sinαsinβ，代值计算可得．
解答：
解：∵锐角α、β满足sinα=
，cosβ=
，
∴cosα=
=
，sinβ=
=
，
∴cos（α-β）=cosαcosβ+sinαsinβ
=
×
+
×
=
故答案为：
| ||
| 5 |
3
| ||
| 10 |
∴cosα=
| 1-sin2α |
2
| ||
| 5 |
| 1-cos2β |
| ||
| 10 |
∴cos（α-β）=cosαcosβ+sinαsinβ
=
2
| ||
| 5 |
3
| ||
| 10 |
| ||
| 5 |
| ||
| 10 |
7
| ||
| 10 |
故答案为：
7
| ||
| 10 |
点评：本题考查两角和与差的三角函数公式，涉及同角三角函数的基本关系，属基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
若函数f（x）=-sin2ωx-6sinωxcosωx+3cos2ωx（ω＞0）的最小正周期为2π，若对任意x∈R都有f（x）-1≤|f（α）-1|，则tanα的值为（ ）
A、
| ||
B、
| ||
C、-
| ||
D、-
|
以茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩（单位：分），已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x，y的值分别为（ ）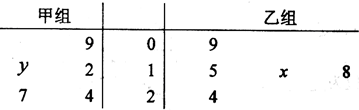
| A、5，2 | B、5，5 |
| C、8，5 | D、8，8 |
对两条不相交的空间直线a与b，必存在平面α，使得（ ）
| A、a?α，b?α |
| B、a?α，b∥α |
| C、a⊥α，b⊥α |
| D、a?α，b⊥α |
命题“若x2＜1，则-1＜x＜1”的逆否命题是（ ）
| A、若x2≥1，则x≥1且x≤-1 |
| B、若-1＜x＜1，则x2＜1 |
| C、若x＞1或x＜-1，则x2＞1 |
| D、若x≥1或x≤-1，则x2≥1 |