Question

【题目】市政府为了促进低碳环保的出行方式，从全市在册的50000辆电动车中随机抽取100辆，委托专业机构免费为它们进行电池性能检测.电池性能分为需要更换、尚能使用、较好、良好四个等级，并分成电动自行车和电动汽车两个群体分别进行统计，样本分布如下图.

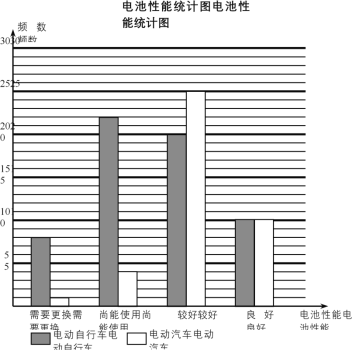
（1）从电池性能较好的电动车中，采用分层抽样的方法随机抽取了9辆，求再从这9辆电动车中随机抽取2辆，至少有1辆为电动汽车的概率；

（2）为提高市民对电动车的使用热情，市政府准备为电动车车主一次性发放补助，标准如下：

①电动自行车每辆补助300元；

②电动汽车每辆补助500元；

③对电池需要更换的电动车每辆额外补助400元.

利用样本估计总体，试估计市政府执行此方案的预算（单位：万元）.

Answer 1

【答案】（1）；（2）2080

【解析】

(1) 根据分层抽样的原理，电动自行车应抽取（辆），电动汽车应抽取（辆），由古典概型以及对立事件概率公式可得，所求概率；（2）设电动车车主能得到的补助为元，则可取，，，，结合组合知识，利用古典概型概率公式,求出各随机变量对应的概率，从而可得分布列，进而利用期望公式可得的数学期望.

（1）根据分层抽样的原理，电动自行车应抽取（辆），

电动汽车应抽取（辆），

则所求概率.

（2）设电动车车主能得到的补助为元，则可取，，，.

，，，，其分布列如下：

	300	500	700	900

电动车车主得到的补助的期望 ，

则估计市政府执行此方案的预算为元.