题目内容
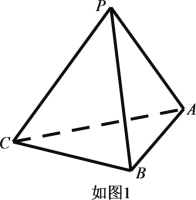
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的正切值.
的正切值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() (2)由
(2)由![]() ,得
,得![]() 平面
平面![]() ,从而
,从而![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,且
所成角,且![]() ,进而当
,进而当![]() 最短时,即
最短时,即![]() 是
是![]() 中点时,
中点时,![]() 最大,由
最大,由![]() 平面
平面![]() ,得
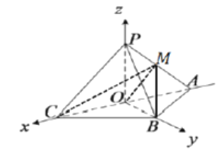
,得![]() ,以
,以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,利用向量法先求出二面角的余弦值,根据同角三角函数关系即可求出正切值.
轴,建立空间直角坐标系,利用向量法先求出二面角的余弦值,根据同角三角函数关系即可求出正切值.
(1 )三棱锥![]() (如图1)的平面展开图(如图2)中
(如图1)的平面展开图(如图2)中
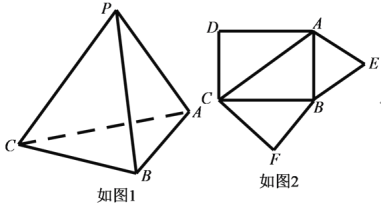
四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,
均为正三角形,
![]()
![]() ,
,
取![]() 中点
中点![]() ,连接
,连接![]() ,
,
则![]() ,
,
且![]() ,
,
![]()
![]() ,
,
又![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]()
(2)由(1)知![]() ,
,
![]() ,
,
![]() 平面
平面![]()
![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,且
所成角,且![]() ,
,
![]() 当
当![]() 最短时,即
最短时,即![]() 是
是![]() 中点时,
中点时,![]() 最大,
最大,
由![]() 平面
平面![]() ,得
,得![]() ,
,
![]() 以
以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,如图:
轴,建立空间直角坐标系,如图:
则![]() ,
,
![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则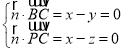 ,取
,取![]() ,得
,得![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
所以![]() ,
,
![]() 二面角
二面角![]() 的正切值为
的正切值为![]() .
.

【题目】某学校高一、高二、高三三个年级共有![]() 名教师,为调查他们的备课时间情况,通过分层抽样获得了
名教师,为调查他们的备课时间情况,通过分层抽样获得了![]() 名教师一周的备课时间,数据如下表(单位:小时).
名教师一周的备课时间,数据如下表(单位:小时).
高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
(1)试估计该校高三年级的教师人数;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲,高二年级选出的人记为乙,求该周甲的备课时间不比乙的备课时间长的概率;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是![]() ,
, ![]() ,
, ![]() (单位:小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位:小时),这三个数据与表格中的数据构成的新样本的平均数记为![]() ,表格中的数据平均数记为
,表格中的数据平均数记为![]() ,试判断
,试判断![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
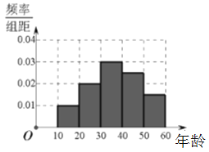
【题目】中国已经成为全球最大的电商市场,但是实体店仍然是消费者接触商品和品牌的重要渠道.某机构随机抽取了年龄介于10岁到60岁的消费者200人,对他们的主要购物方式进行问卷调查.现对调查对象的年龄分布及主要购物方式进行统计,得到如下图表:
主要购物方式 年龄阶段 | 网络平台购物 | 实体店购物 | 总计 |
40岁以下 | 75 | ||
40岁或40岁以上 | 55 | ||
总计 |
(1)根据已知条件完成上述列联表,并据此资料,能否在犯错误的概率不超过![]() 的前提下,认为消费者主要的购物方式与年龄有关?
的前提下,认为消费者主要的购物方式与年龄有关?
(2)用分层抽样的方法从通过网络平台购物的消费者中随机抽取8人,然后再从这8名消费者中抽取5名进行答谢.设抽到的消费者中40岁以下的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: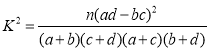 ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】2017年5月27日当今世界围棋排名第一的柯洁在与![]() 的人机大战中中盘弃子认输,至此柯洁与
的人机大战中中盘弃子认输,至此柯洁与![]() 的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

(1)请根据已知条件完成下面![]() 列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)为了进一步了解“围棋迷”的围棋水平,从“围棋迷”中按性别分层抽样抽取5名学生组队参加校际交流赛,首轮该校需派两名学生出赛,若从5名学生中随机抽取2人出赛,求2人恰好一男一女的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()