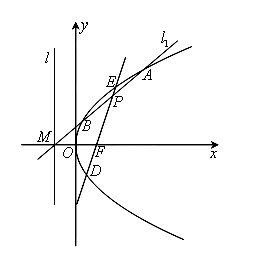
题目内容
如图,设抛物线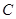 :
: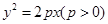 的焦点为
的焦点为 ,准线为
,准线为 ,过准线
,过准线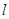 上一点
上一点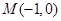 且斜率为
且斜率为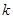 的直线
的直线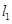 交抛物线
交抛物线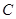 于
于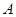 ,
,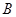 两点,线段
两点,线段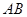 的中点为
的中点为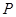 ,直线
,直线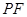 交抛物线
交抛物线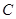 于
于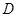 ,
,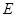 两点.
两点.
(1)求抛物线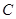 的方程及
的方程及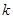 的取值范围;
的取值范围;
(2)是否存在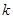 值,使点
值,使点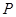 是线段
是线段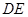 的中点?若存在,求出
的中点?若存在,求出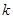 值,若不存在,请说明理由.
值,若不存在,请说明理由.
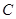 :
: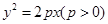 的焦点为
的焦点为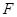 ,准线为
,准线为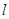 ,过准线
,过准线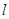 上一点
上一点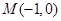 且斜率为
且斜率为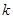 的直线
的直线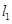 交抛物线
交抛物线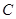 于
于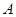 ,
,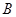 两点,线段
两点,线段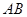 的中点为
的中点为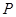 ,直线
,直线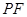 交抛物线
交抛物线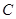 于
于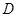 ,
,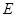 两点.
两点. (1)求抛物线
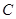 的方程及
的方程及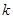 的取值范围;
的取值范围;(2)是否存在
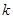 值,使点
值,使点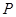 是线段
是线段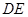 的中点?若存在,求出
的中点?若存在,求出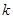 值,若不存在,请说明理由.
值,若不存在,请说明理由. 
(1)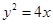 ,
,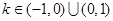 ;(2)不存在.参考解析
;(2)不存在.参考解析
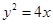 ,
,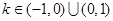 ;(2)不存在.参考解析
;(2)不存在.参考解析试题分析:(1)由准线
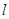 上一点
上一点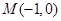 ,所以可以求得
,所以可以求得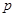 的值,即可取得抛物线的方程.由于直线与抛物线有两个交点,所以联立方程消去y,需要判别式大于零即可得到k的取值范围,又由于k等于零时没有两个交点,所以应排除,即可得到结论.
的值,即可取得抛物线的方程.由于直线与抛物线有两个交点,所以联立方程消去y,需要判别式大于零即可得到k的取值范围,又由于k等于零时没有两个交点,所以应排除,即可得到结论.(2)是否存在
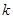 值,使点
值,使点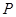 是线段
是线段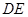 的中点.由直线AB的方程联立抛物线的方程,即可求得AB中点P的坐标.从而写出PF的方程再联立抛物线的方程,对比DE的中点是否与AB的中点相同.即可得到答案.
的中点.由直线AB的方程联立抛物线的方程,即可求得AB中点P的坐标.从而写出PF的方程再联立抛物线的方程,对比DE的中点是否与AB的中点相同.即可得到答案.(1)由已知得
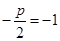 ,∴
,∴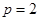 .∴抛物线方程为
.∴抛物线方程为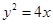 . 2分
. 2分设
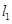 的方程为
的方程为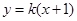 ,
,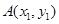 ,
,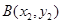 ,
,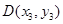 ,
,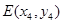 ,
,由
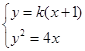 得
得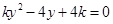 . 4分
. 4分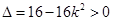 ,解得
,解得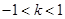 ,注意到
,注意到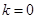 不符合题意,
不符合题意,所以
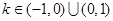 . 5分
. 5分(2)不存在
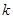 值,使点
值,使点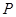 是线段
是线段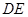 的中点.理由如下: 6分
的中点.理由如下: 6分有(1)得
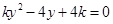 ,所以
,所以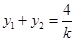 ,所以
,所以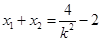 ,
,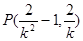 ,直线
,直线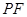 的方程为
的方程为 . 8分
. 8分由
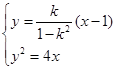 得
得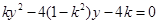 ,
,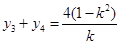 . 10分
. 10分当点
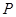 为线段
为线段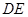 的中点时,有
的中点时,有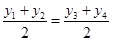 ,即
,即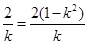 ,因为
,因为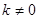 ,所以此方程无实数根.因此不存在
,所以此方程无实数根.因此不存在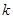 值,使点
值,使点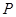 是线段
是线段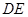 的中点. 12分
的中点. 12分
练习册系列答案
相关题目
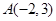 在抛物线C:
在抛物线C: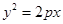 的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )
的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )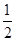
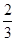
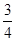
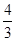
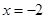 ,则抛物线的方程是( )
,则抛物线的方程是( )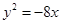
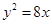
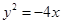
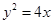
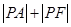 的最小值及此时P点的坐标.
的最小值及此时P点的坐标. 上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当
上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当 时,
时, 的最小值是( )
的最小值是( )



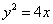 的焦点到双曲线
的焦点到双曲线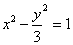 的渐近线的距离是( )
的渐近线的距离是( )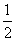

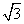
 的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且
的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且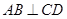 ,则
,则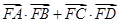 的最大等于 ( )
的最大等于 ( )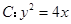 的焦点为
的焦点为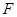 ,
,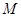 为抛物线
为抛物线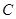 上一点,且点
上一点,且点 .
. 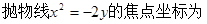 。
。