题目内容
已知定义域为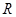 的函数
的函数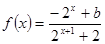 是奇函数.
是奇函数.
(Ⅰ)求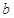 的值;
的值;
(Ⅱ)证明函数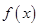 在
在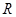 上是减函数.
上是减函数.
(1)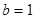 ,(2)详见解析
,(2)详见解析
解析试题分析:(1)根据定义域能取到零的奇函数过原点,即 解方程可求得
解方程可求得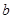 值;(2)利用函数单调性的定义证明函数
值;(2)利用函数单调性的定义证明函数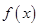 在
在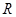 上是减函数,分四步:第一“取值”,第二“作差、变形”,第三“定号”、第四“下结论”,即证明函数单调性的“四部曲”.
上是减函数,分四步:第一“取值”,第二“作差、变形”,第三“定号”、第四“下结论”,即证明函数单调性的“四部曲”.
试题解析:(Ⅰ)∵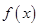 是奇函数,所以
是奇函数,所以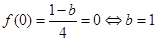 (经检验符合题设)
(经检验符合题设)
(Ⅱ)由(1)知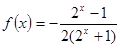 .对
.对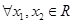 ,当
,当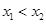 时,总有
时,总有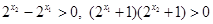 ,
,
∴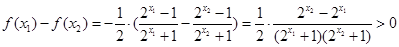 ,
,
即 .
.
∴函数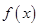 在
在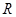 上是减函数.
上是减函数.
考点:奇函数的性质应用,函数单调性的证明.

练习册系列答案
相关题目
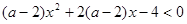 对一切
对一切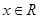 恒成立,试确定实数
恒成立,试确定实数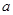 的取值范围.
的取值范围.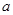 为实数,函数
为实数,函数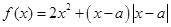 .
.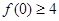 ,求
,求 的最小值.
的最小值. 毫克)与时间
毫克)与时间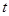 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,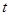 的函数关系式为
的函数关系式为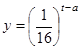 (
(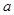 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题: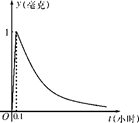
 }的前n项和为为
}的前n项和为为 ,且
,且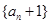 是等比数列;
是等比数列;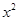 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥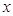 千件,需另投入成本为
千件,需另投入成本为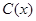 (万元),当年产量不足80千件时,
(万元),当年产量不足80千件时,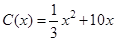 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,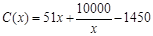 (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完. (万元)关于年产量
(万元)关于年产量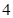 元,并且每件商品需向总店交
元,并且每件商品需向总店交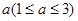 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为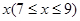 元时,一年的销售量为
元时,一年的销售量为 万件.
万件.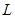 (万元)与每件商品的售价
(万元)与每件商品的售价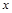 的函数关系式
的函数关系式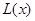 ;
;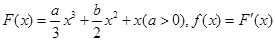 ,若
,若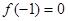 且对任意实数
且对任意实数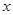 均有
均有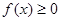 成立.
成立.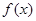 表达式;
表达式;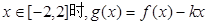 是单调函数,求实数
是单调函数,求实数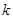 的取值范围.
的取值范围.