题目内容
记数列{ }的前n项和为为
}的前n项和为为 ,且
,且 +
+ +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.
(1)求证:数列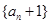 是等比数列;
是等比数列;
(2)已知2是函数f(x)=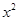 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥ 对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
(Ⅰ)见解析;(II) 的取值范围
的取值范围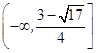 .
.
解析试题分析:(Ⅰ)利用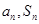 间的关系解答,写出
间的关系解答,写出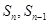 相减,然后根据等比数列定义确定答案;(II)利用(Ⅰ)的结果和等比数列通项公式求出
相减,然后根据等比数列定义确定答案;(II)利用(Ⅰ)的结果和等比数列通项公式求出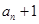 ,然后构造出不等式
,然后构造出不等式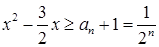 ,求出
,求出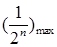 解关于
解关于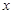 的不等式得出答案.
的不等式得出答案.
试题解析:(Ⅰ) 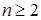 时,
时,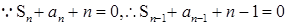 ,两式相减可得,
,两式相减可得,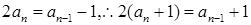 ,
,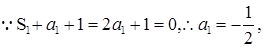
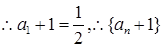 是以
是以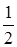 为首项,
为首项,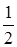 为公比的等比数列. 6分
为公比的等比数列. 6分
(II)由(Ⅰ)可得,
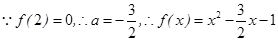 ,
,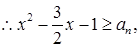 即
即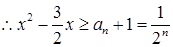 ,
,
即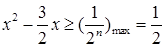 在
在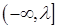 上恒成立,由
上恒成立,由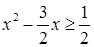 ,即
,即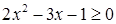 ,
, 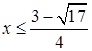 或
或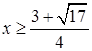 ,
,  ,
,
即所求 的取值范围
的取值范围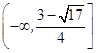 . 12分
. 12分
考点:等比数列定义和通项公式、函数最值、一元二次不等式解法.

练习册系列答案
相关题目
 ; (2)
; (2)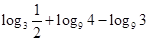 .
.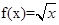 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式. 的值;
的值; 的值.
的值.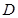 上的函数
上的函数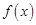 ,如果满足:对任意
,如果满足:对任意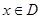 ,存在常数
,存在常数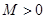 ,使得
,使得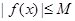 成立,则称
成立,则称 是
是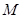 称为函数
称为函数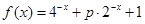 ,
,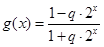 .
.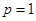 时,求函数
时,求函数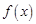 在
在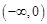 上的值域,并判断函数
上的值域,并判断函数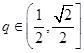 ,函数
,函数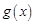 在
在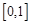 上的上界是
上的上界是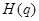 ,求
,求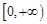 上是以
上是以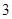 为上界的有界函数, 求实数
为上界的有界函数, 求实数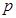 的取值范围.
的取值范围.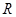 的函数
的函数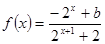 是奇函数.
是奇函数.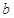 的值;
的值;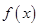 在
在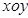 ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在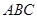 段可近似地用解析式
段可近似地用解析式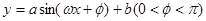 来描述,从
来描述,从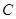 点走到今天的
点走到今天的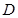 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且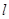 :
: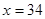 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里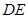 段与
段与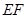 段是股价延续
段是股价延续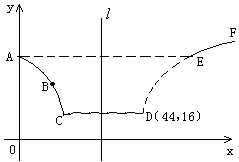
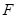 。现在老张决定取点
。现在老张决定取点
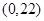 ,点
,点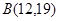 ,点
,点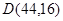 来确定解析式中的常数
来确定解析式中的常数 ,
,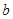 ,
,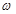 ,
,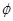 ,并且求得
,并且求得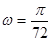 。
。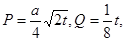 其中
其中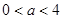 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),