题目内容
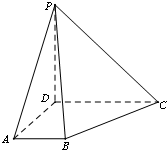
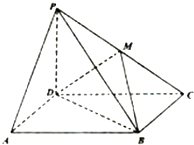
如图,点P为平行四边形ABCD外一点,且PD⊥平面ABCD,M为PC中点.
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.

(1)设AC∩BD=H,连接EH,
∵H为平行四边形ABCD对角线的交点,∴H为AC中点,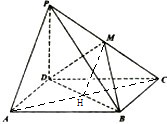
又∵M为PC中点,∴MH为△PAC中位线,
可得MH∥PA,
MH?平面MBD,PA?平面MBD,
所以PA∥平面MBD.
(2)∵PD⊥平面ABCD,AD?平面ABCD,
∴PD⊥AD,
又∵AD⊥PB,PD∩PB=D,
∴AD⊥平面PDB,结合BD?平面PDB,得AD⊥BD
∵PD⊥BD,且PD、AD是平面PAD内的相交直线
∴BD⊥平面PAD.
∵H为平行四边形ABCD对角线的交点,∴H为AC中点,

又∵M为PC中点,∴MH为△PAC中位线,
可得MH∥PA,
MH?平面MBD,PA?平面MBD,
所以PA∥平面MBD.
(2)∵PD⊥平面ABCD,AD?平面ABCD,
∴PD⊥AD,
又∵AD⊥PB,PD∩PB=D,
∴AD⊥平面PDB,结合BD?平面PDB,得AD⊥BD
∵PD⊥BD,且PD、AD是平面PAD内的相交直线
∴BD⊥平面PAD.

练习册系列答案
相关题目