题目内容
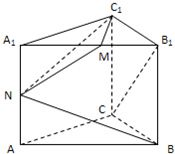
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别为A1B1、A1A的中点.
(Ⅰ)求cos<
,
>的值;
(Ⅱ)求证:BN⊥平面C1MN;
(Ⅲ)求点B1到平面C1MN的距离.
(Ⅰ)求cos<
| BA1 |
| CB1 |
(Ⅱ)求证:BN⊥平面C1MN;
(Ⅲ)求点B1到平面C1MN的距离.

(Ⅰ)以CA所在直线为x轴,以CB所在直线为y轴,以CC1所在直线为z轴建立空间坐标系.
则A(1,0,0),B(0,1,0),A1(1,0,2),B1(0,1,2),C1(0,0,2),M(
,
,2),
N(1,0,1),
∵
=(1,-1,2),
=(0,1,2).
∴cos<
,
>=
=
=
.
(Ⅱ)∵
=(1,-1,1),
=(
,
,0),
=(1,0,-1),
∴
=
-
+0=0,
•
=1-0-1=0,∴
⊥
,
⊥
,
∴BN⊥平面C1MN.
(Ⅲ)设点B1到平面C1MN的距离为h,∵VB1-C1MN=VN-C1MB1,
∴
×(
MN•MC1)h=
×(
B1M•C1M) NA1,
即
×(
•
)h=
×(
•
•
)×1,∴h=
.
则A(1,0,0),B(0,1,0),A1(1,0,2),B1(0,1,2),C1(0,0,2),M(
| 1 |
| 2 |
| 1 |
| 2 |
N(1,0,1),
∵
| BA1 |
| CB1 |
∴cos<
| BA1 |
| CB1 |
| ||||
|
|
| (1,-1,2)•(0,1,2) | ||||
|
| ||
| 10 |
(Ⅱ)∵
| BN |
| C1M |
| 1 |
| 2 |
| 1 |
| 2 |
| C1N |
∴
| BN |
| •C1M |
| 1 |
| 2 |
| 1 |
| 2 |
| BN |
| C1N |
| BN |
| C1M |
| BN |
| C1N |
∴BN⊥平面C1MN.
(Ⅲ)设点B1到平面C1MN的距离为h,∵VB1-C1MN=VN-C1MB1,
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
即
| 1 |
| 3 |
| 1 |
| 2 |
1+
|
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 3 |

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
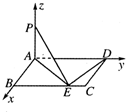

 底面ABCD,PA=AD=DC=
底面ABCD,PA=AD=DC=