Question

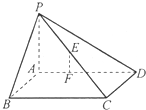
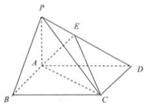
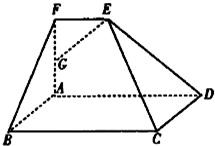
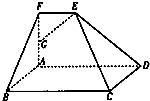
如图，在多面体ABCDEF中，四边形ABCD是正方形，FA⊥平面ABCD，EF∥BC，FA=2，AD=3，∠ADE=45°，点G是FA的中点．
（1）求证：EG⊥平面CDE；
（2）在棱BC是否存在点M，使GM∥平面CDE，若存在，找出点M；若不存在，说明理由．

Answer 1

证明：（1）∵EF∥BC，AD∥BC，∴EF∥AD．
在四边形ADEF中，由FA=2，AD=3，∠ADE=45°，可证得EG⊥DE，
又由FA⊥平面ABCD，得AF⊥CD，
∵正方形ABCD中CD⊥AD，∴CD⊥平面ADEF，
∵EG?平面ADEF，∴CD⊥EG，
∵CD∩DE=D，∴EG⊥平面CDE；…（6分）
（2）在BC存在点M，BC=3BM，使GM∥平面CDE
取DE中点H，连接GM、GH、CH，
∵在梯形ADEF中，G是AF中点，
∴GH=

1

2

(AD+EF=2)，GH∥AD，
∵BC∥AD，BC=AD=3，BC=3BM，∴CM=2=GH，GH∥CM，
∴四边形CHGM是平行四边形
∴GM∥CH，∴GM∥平面CDE．