题目内容
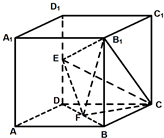
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
(1)求证:直线BD1∥平面PAC;
(2)求证:平面PAC⊥平面BDD1;
(3)求证:直线PB1⊥平面PAC.
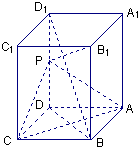
(1)求证:直线BD1∥平面PAC;
(2)求证:平面PAC⊥平面BDD1;
(3)求证:直线PB1⊥平面PAC.

(1)设AC和BD交于点O,连PO,
由P,O分别是DD1,BD的中点,故PO∥BD1,
所以直线BD1∥平面PAC.
(2)长方体ABCD-A1B1C1D1中,AB=AD=1,
底面ABCD是正方形,则AC⊥BD
又DD1⊥面ABCD,则DD1⊥AC,
所以AC⊥面BDD1,则平面PAC⊥平面BDD1
(3)PC2=2,PB12=3,B1C2=5,所以△PB1C是直角三角形.PB1⊥PC,
同理PB1⊥PA,所以直线PB1⊥平面PAC.(12分)
由P,O分别是DD1,BD的中点,故PO∥BD1,
所以直线BD1∥平面PAC.
(2)长方体ABCD-A1B1C1D1中,AB=AD=1,
底面ABCD是正方形,则AC⊥BD
又DD1⊥面ABCD,则DD1⊥AC,
所以AC⊥面BDD1,则平面PAC⊥平面BDD1
(3)PC2=2,PB12=3,B1C2=5,所以△PB1C是直角三角形.PB1⊥PC,
同理PB1⊥PA,所以直线PB1⊥平面PAC.(12分)

练习册系列答案
相关题目