题目内容
【题目】要在如图所示的花圃中的5个区域中种入4种颜色不同的花,要求相邻区域不同色,有种不同的种法(用数字作答). 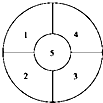
【答案】72
【解析】解:首先,区域1可取4种颜色任何一种色,有 ![]() 种,区域2只能取除1以外的颜色有
种,区域2只能取除1以外的颜色有 ![]() 种; 区域4与区域2不相邻,也可取除1以外的3种颜色,有
种; 区域4与区域2不相邻,也可取除1以外的3种颜色,有 ![]() 种;
种;
区域5有两种可能:①区域2,区域4取同一色,有 ![]() 种;②区域2,区域4取不同色,区域5只有一色可取,有
种;②区域2,区域4取不同色,区域5只有一色可取,有 ![]() 种方法;
种方法;
区域3也有2种可能:若区域2,区域4取同一色,有 ![]() 种取法;若区域2,区域4取不同色,区域5只有一色可取,有
种取法;若区域2,区域4取不同色,区域5只有一色可取,有 ![]() 种方法;
种方法;
区域2、区域4共 ![]() ×
× ![]() =3×3=9取法中,3种取法是同一色的,6种取法是不同色的;
=3×3=9取法中,3种取法是同一色的,6种取法是不同色的;
所以,共有着色方法 ![]() ×3×
×3× ![]() ×
× ![]() +
+ ![]() ×6×
×6× ![]() ×
× ![]()
=4×3×2×2+4×6×1×1
=48+24
=72种.
故答案为:72.
区域1可取4种颜色任何一种色,有 ![]() 种,区域2只能取除区域1以外的颜色有
种,区域2只能取除区域1以外的颜色有 ![]() 种,区域4与区域2不相邻,有
种,区域4与区域2不相邻,有 ![]() 种;再对区域5与区域3分类讨论,最后利用乘法原理与加法原理运算即可求得答案.
种;再对区域5与区域3分类讨论,最后利用乘法原理与加法原理运算即可求得答案.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目