ЬтФПФкШн
ЁОЬтФПЁПЮКНњЪБЦкЪ§бЇМвСѕЛедкЮЊЁЖОХеТЫуЪѕЁЗзїзЂЪБЃЌЬсГіРћгУЁАФВКЯЗНИЧЁБНтОіЧђЬхЬхЛ§ЃЌЁАФВКЯЗНИЧЁБгЩЭъШЋЯрЭЌЕФЫФИіЧњУцЙЙГЩЃЌЯрЖдЕФСНИіЧњУцдкЭЌвЛдВжљЕФВрУцЩЯЃЌе§ЪгЭМКЭВрЪгЭМЖМЪЧдВЃЌУПвЛИіЫЎЦННиУцЖМЪЧе§ЗНаЮЃЌКУЫЦСНИіПлКЯ(ФВКЯ)дквЛЦ№ЕФЗНаЮЩЁ(ЗНИЧ)ЃЎЖўАйЖрФъКѓЃЌФЯББГЏЪБЦкЪ§бЇМвзцдкЧАШЫбаОПЕФЛљДЁЩЯЬсГіСЫЁЖзцдРэЁЗЃКЁАУнЪЦМШЭЌЃЌдђЛ§ВЛШнвьЁБЃЎвтЫМЪЧЃКСНЕШИпСЂЗНЬхЃЌШєдкУПвЛЕШИпДІЕФНиУцЛ§ЖМЯрЕШЃЌдђСНСЂЗНЬхЬхЛ§ЯрЕШЃЎШчЭМгавЛФВКЯЗНИЧЃЌЦфе§ЪгЭМгыВрЪгЭМЖМЪЧАыОЖЮЊ![]() ЕФдВЃЌе§БпаЮ
ЕФдВЃЌе§БпаЮ![]() ЪЧЮЊЬхЯжЦфжБЙладЫљзїЕФИЈжњЯпЃЌИљОнзцдРэЃЌИУФВКЯЗНИЧЬхЛ§ЮЊ__________ЃЎ
ЪЧЮЊЬхЯжЦфжБЙладЫљзїЕФИЈжњЯпЃЌИљОнзцдРэЃЌИУФВКЯЗНИЧЬхЛ§ЮЊ__________ЃЎ

ЁОД№АИЁП![]()
ЁОНтЮіЁП
ШЁСЂЗНЬхгыФкЧаЕФФВКЯЗНИЧЕФ![]() РДзібаОПЃЌгЩзцдРэПЩжЊЃЌгыСЂЗНЬхЭЌЕзЕШИпе§ЫФРтзЖЬхЛ§гыЗНИЧВю(СЂЗНЬхжЎФкФВКЯЗНИЧжЎЭтВП)ЕФЬхЛ§ЯрЕШЃЌМДПЩЧѓГіФВКЯЗНИЧЬхЛ§.
РДзібаОПЃЌгЩзцдРэПЩжЊЃЌгыСЂЗНЬхЭЌЕзЕШИпе§ЫФРтзЖЬхЛ§гыЗНИЧВю(СЂЗНЬхжЎФкФВКЯЗНИЧжЎЭтВП)ЕФЬхЛ§ЯрЕШЃЌМДПЩЧѓГіФВКЯЗНИЧЬхЛ§.
ШЁСЂЗНЬхгыФкЧаЕФФВКЯЗНИЧЕФ![]() РДзібаОПЃЌЩшдкИпЮЊ
РДзібаОПЃЌЩшдкИпЮЊ![]() ДІЕФвЛИіЦНУцНиСНИіСЂЬхЃЌНиУцШчЭМвѕгАВПЗжЫљЪОЃЌ
ДІЕФвЛИіЦНУцНиСНИіСЂЬхЃЌНиУцШчЭМвѕгАВПЗжЫљЪОЃЌ
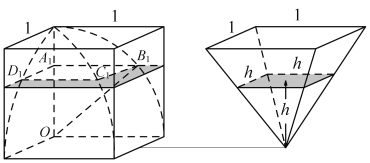
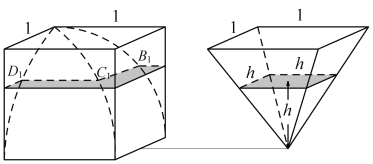
гыИУСЂЗНЬхЕШЕзЕШИпЕФЫФРтзЖЕФНиУцЪЧе§ЗНаЮЃЌЦфУцЛ§ЪЧ![]() ЃЌ
ЃЌ
ЗНИЧВю(СЂЗНЬхжЎФкФВКЯЗНИЧжЎЭтВП)ЩЯЕФНиУцЪЧЙеГпаЮЃЌЦфУцЛ§МЦЫуШчЯТЃК
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЫљвдЭМжавѕгАЕФЙеаЮУцЛ§![]() ЃЌЯдШЛЕШгке§ЫФРтзЖНиУцУцЛ§ЃЌ
ЃЌЯдШЛЕШгке§ЫФРтзЖНиУцУцЛ§ЃЌ
ДгЖјгЩзцдРэПЩжЊЃЌе§ЫФРтзЖЬхЛ§гыЗНИЧВюЕФЬхЛ§ЯрЕШЃЌ
ЫљвдЗНИЧВюЕФЬхЛ§ЮЊ![]() ЃЌ
ЃЌ
ДгЖјПЩЕУФВКЯЗНИЧЬхЛ§ЮЊ![]() .
.
ЙЪД№АИЮЊЃК![]()

 ЦєЖЋаЁЬтзївЕБОЯЕСаД№АИ
ЦєЖЋаЁЬтзївЕБОЯЕСаД№АИЁОЬтФПЁПФГЙЄГЇЕФ![]() ,
,![]() ,
,![]() Ш§ИіВЛЭЌГЕМфЩњВњЭЌвЛВњЦЗЕФЪ§СП(ЕЅЮЛ:Мў)ШчЯТБэЫљЪО.жЪМьШЫдБгУЗжВуГщбљЕФЗНЗЈДгетаЉВњЦЗжаЙВГщШЁ6МўбљЦЗНјааМьВт:
Ш§ИіВЛЭЌГЕМфЩњВњЭЌвЛВњЦЗЕФЪ§СП(ЕЅЮЛ:Мў)ШчЯТБэЫљЪО.жЪМьШЫдБгУЗжВуГщбљЕФЗНЗЈДгетаЉВњЦЗжаЙВГщШЁ6МўбљЦЗНјааМьВт:
ГЕМф |
|
|
|
Ъ§СП | 50 | 150 | 100 |
(1)Чѓет6МўбљЦЗжаРДзд![]() ,
,![]() ,
,![]() ИїГЕМфВњЦЗЕФЪ§СП;
ИїГЕМфВњЦЗЕФЪ§СП;
(2)Шєдкет6МўбљЦЗжаЫцЛњГщШЁ2МўНјааНјвЛВНМьВт,Чѓет2МўВњЦЗРДздЯрЭЌГЕМфЕФИХТЪ.