题目内容
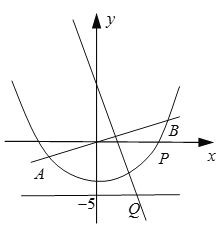
【题目】已知抛物线![]() :
:![]() 上的点到焦点的距离最小值为1.
上的点到焦点的距离最小值为1.
(1)求![]() 的值;
的值;
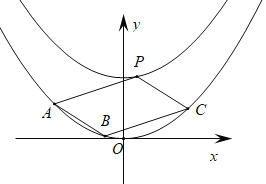
(2)若点![]() 在曲线
在曲线![]() :
:![]() 上,且在曲线
上,且在曲线![]() 上存在三点
上存在三点![]() ,
,![]() ,
,![]() ,使得四边形
,使得四边形![]() 为平行四边形.求平行四边形
为平行四边形.求平行四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
【答案】(1)![]() (2)最小值为
(2)最小值为![]() .
.
【解析】
(1)由抛物线定义,结合抛物线的几何性质可知![]() 到准线
到准线![]() 的距离为最小值,即可求得
的距离为最小值,即可求得![]() 的值;
的值;
(2)方法一:设出直线![]() 的方程,并讨论斜率是否存在.联立直线与抛物线方程,结合韦达定理表示出
的方程,并讨论斜率是否存在.联立直线与抛物线方程,结合韦达定理表示出![]() 中点
中点![]() 的坐标.将点
的坐标.将点![]() 代入曲线
代入曲线![]() 可得
可得![]() .根据平行四边形性质可知
.根据平行四边形性质可知![]() ,
,![]() 关于点
关于点![]() 对称,即可表示出B点坐标,可得方程
对称,即可表示出B点坐标,可得方程![]() .利用三角形面积公式表示出平行四边形
.利用三角形面积公式表示出平行四边形![]() 的面积
的面积![]() ,根据等量关系即可求得面积的最小值.
,根据等量关系即可求得面积的最小值.
方法二: 设![]() ,
,![]() ,表示出直线
,表示出直线![]() 的方程,由点
的方程,由点![]() 在曲线
在曲线![]() 上,可得
上,可得![]() .由
.由![]() ,
,![]() 关于点
关于点![]() 对称,可得B点坐标,将B的坐标代入抛物线方程,可得
对称,可得B点坐标,将B的坐标代入抛物线方程,可得![]() 的等量关系.根据三角形面积公式表示出平行四边形
的等量关系.根据三角形面积公式表示出平行四边形![]() 的面积
的面积![]() ,进而由不等式关系即可求得最小值.
,进而由不等式关系即可求得最小值.
(1)根据抛物线的定义可知,抛物线上的点到焦点的距离等于到准线的距离
抛物线上的点到焦点的距离最小值为1
即![]() 到准线
到准线![]() 的距离为1
的距离为1
即![]() ,所以
,所以![]()
(2)方法一:设直线![]() :
:![]() ,
,
当![]() 不存在时,此时直线
不存在时,此时直线![]() 为竖直线,与抛物线只有一个交点,故舍去.
为竖直线,与抛物线只有一个交点,故舍去.
设![]() ,
,![]()
联立方程![]() ,得
,得![]()
![]() ,
,![]() .
.
故线段![]() 中点
中点![]()
而点![]() 在曲线
在曲线![]() :
:![]() 上
上
故![]()
若要满足四边形![]() 为平行四边形,则
为平行四边形,则![]() ,
,![]() 关于点
关于点![]() 对称.则
对称.则![]() .又点
.又点![]() 在抛物线
在抛物线![]() 上,
上,
故满足方程![]() ,即
,即![]() ①
①
![]()
![]() ,
,
代入①得:![]()
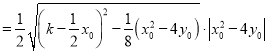 ,
,
所以![]()
所以平行四边形![]() 的面积
的面积![]() 的最小值为
的最小值为![]() .
.
方法二:设![]() ,
,![]() ,
,
直线![]() :
:![]() ,点
,点![]() 在曲线
在曲线![]() :
:![]() 上,
上,
故![]() .线段
.线段![]() 中点
中点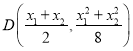 ,若要满足四边形
,若要满足四边形![]() 为平行四边形,
为平行四边形,
则![]() ,
,![]() 关于点
关于点![]() 对称,则
对称,则 .又点
.又点![]() 在抛物线
在抛物线![]() 上
上
故满足方程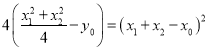 ,即
,即![]() ①
①
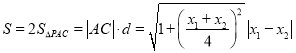
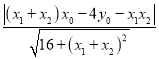

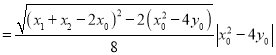
![]() .
.
所以平行四边形![]() 的面积
的面积![]() 的最小值为
的最小值为![]() .
.

 优学名师名题系列答案
优学名师名题系列答案【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
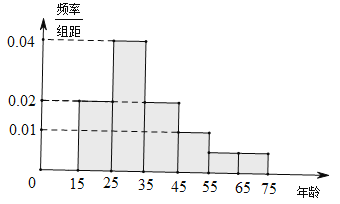
根据上表的数据得到如下的散点图.
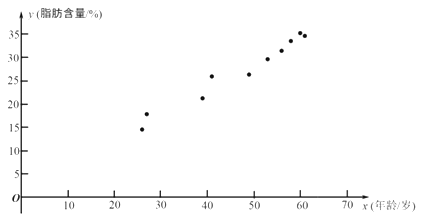
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(i)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
附:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数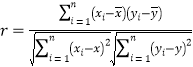
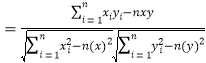
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为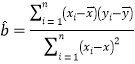 ,
,![]() .
.
【题目】某农户计划种植莴笋和西红柿,种植面积不超过![]() 亩,投入资金不超过
亩,投入资金不超过![]() 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为____万元