题目内容
1.如图是某简单组合体的三视图,则该组合体的体积为36$\sqrt{3}$(π+2).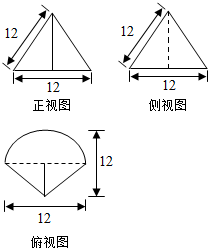
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥和半圆锥的组合体,求出底面面积,代入棱锥体积公式,可得答案.
解答 解:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥和半圆锥的组合体,
锥体的底面面积S=$\frac{1}{2}$π$(\frac{12}{2})^{2}$+$\frac{1}{2}×12×(12-\frac{12}{2})$=18π+36,
锥体的高h=6$\sqrt{3}$,
故锥体的体积V=$\frac{1}{3}$Sh=36$\sqrt{3}$(π+2),
故答案为:36$\sqrt{3}$(π+2);
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.二项式$(\frac{1}{{\sqrt{x}}}-{x^2}{)^{10}}$的展开式中的常数项是( )
| A. | -45 | B. | -10 | C. | 45 | D. | 65 |
9.设P为双曲线 C:x2-y2=1的一点,F1,F2分别为双曲线C的左、右焦点,若cos∠F1PF2=$\frac{1}{3}$,则△PF1F2的内切圆的半径为( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{3}$-1 | D. | $\sqrt{3}$+1 |
6.已知f(x)=cos(ωx+$\frac{π}{6}$)(ω>0)的图象与直线y=1的两个交点的最短距离是π,要得到y=f(x)的图象,只需要把y=sinωx的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
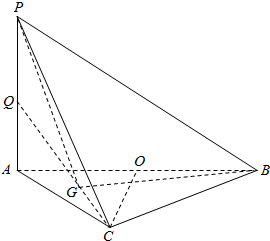 如图所示:在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,O,Q分别为AB,PA的中点,G为△AOC的重心,AC=$\sqrt{3}$,∠ABC=30°
如图所示:在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,O,Q分别为AB,PA的中点,G为△AOC的重心,AC=$\sqrt{3}$,∠ABC=30°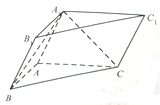 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.