题目内容
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;
④f(0)f(3)<0.
其中正确结论的序号是( )
| A.①③ | B.①④ |
| C.②③ | D.②④ |
C
解析

练习册系列答案
相关题目
设点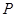 在曲线
在曲线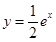 上,点
上,点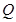 在曲线
在曲线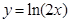 上,则
上,则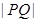 的最小值为( )
的最小值为( )
A.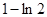 | B.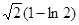 | C.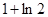 | D.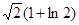 |
已知曲线y=x4+ax2+1在点(-1,a+2)处切线的斜率为8,则a等于( )
| A.9 | B.6 | C.-9 | D.-6 |
已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(1)等于( )
| A.-e | B.-1 | C.1 | D.e |
函数f(x)=x+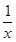 在x>0时有 ( ).
在x>0时有 ( ).
| A.极小值 | B.极大值 |
| C.既有极大值又有极小值 | D.极值不存在 |
设f0(x)=cos x,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈
N,则f2 011(x)等于 ( ).
| A.sin x | B.-sin x |
| C.cos x | D.-cos x |
一物体的运动方程为s=3+t2,则在时间段[2,2.1]内相应的平均速度为( ).
| A.4.11 | B.4.01 |
| C.4.0 | D.4.1 |
质点M的运动方程为s=2t2-2,则在时间段[2,2+Δt]内的平均速度为( ).
| A.8+2Δt | B.4+2Δt | C.7+2Δt | D.-8+2Δt |
若存在过点(1,0)的直线与曲线y=x3和y=ax2+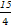 x-9都相切,则a等于( )
x-9都相切,则a等于( )
A.-1或-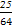 | B.-1或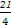 |
C.- 或- 或-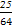 | D.- 或7 或7 |