题目内容
函数f(x)=x+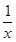 在x>0时有 ( ).
在x>0时有 ( ).
| A.极小值 | B.极大值 |
| C.既有极大值又有极小值 | D.极值不存在 |
A
解析

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
设曲线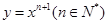 在点(1,1)处的切线与
在点(1,1)处的切线与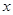 轴的交点的横坐标为
轴的交点的横坐标为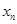 ,则
,则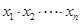 的值为
的值为
A.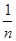 | B.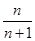 | C.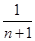 | D.1 |
已知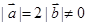 ,且关于
,且关于 的函数
的函数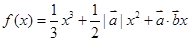 在
在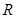 上有极值,则向量
上有极值,则向量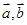 的夹角范围是( )
的夹角范围是( )
A.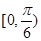 | B.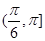 | C.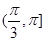 | D.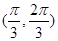 |
下面四图都是在同一坐标系中某三次函数及其导函数的图像,其中一定不正确的序号是( )
| A.①② | B.③④ | C.①③ | D.①④ |
函数f(x)的定义域为(0,+∞),且f(x)>0,f′(x)>0,则函数y=xf(x)( )
| A.存在极大值 | B.存在极小值 |
| C.是增函数 | D.是减函数 |
在函数y=x3-9x的图象上,满足在该点处的切线的倾斜角小于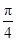 ,且横、纵坐标都为整数的点的个数是( )
,且横、纵坐标都为整数的点的个数是( )
| A.0 | B.1 | C.2 | D.3 |
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;
④f(0)f(3)<0.
其中正确结论的序号是( )
| A.①③ | B.①④ |
| C.②③ | D.②④ |
已知定义域为R的奇函数f(x)的导函数为f′(x),当x≠0时,f′(x)+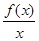 >0,若a=
>0,若a=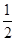 f
f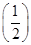 ,b=-2f(-2),c=ln
,b=-2f(-2),c=ln 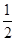 f(ln 2),则下列关于a,b,c的大小关系正确的是( )
f(ln 2),则下列关于a,b,c的大小关系正确的是( )
| A.a>b>c | B.a>c>b |
| C.c>b>a | D.b>a>c |
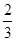 上移动,设点P处切线的倾斜角为α,则角α的取值范围是 ( ).
上移动,设点P处切线的倾斜角为α,则角α的取值范围是 ( ).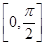
 ∪
∪