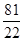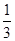题目内容
设f0(x)=cos x,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈
N,则f2 011(x)等于 ( ).
| A.sin x | B.-sin x |
| C.cos x | D.-cos x |
A
解析

练习册系列答案
相关题目
已知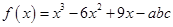 ,
,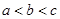 ,且
,且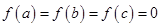 .现给出如下结论:
.现给出如下结论:
①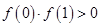 ;②
;②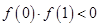 ;③
;③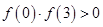 ;④
;④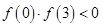 .
.
其中正确结论的序号是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
若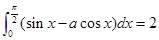 ,则实数
,则实数 等于( )
等于( )
A.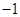 | B.1 | C.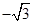 | D.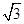 |
函数y=xcos x-sin x在下面哪个区间内是增函数 ( ).
A.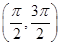 | B.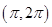 | C.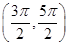 | D.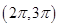 |
函数f(x)=xcos x-sin x在下面哪个区间内是增函数 ( ).
A.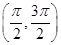 | B.(π,2π) |
C.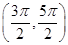 | D.(2π,3π) |
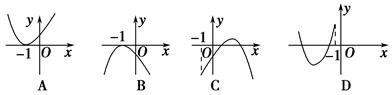
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;
④f(0)f(3)<0.
其中正确结论的序号是( )
| A.①③ | B.①④ |
| C.②③ | D.②④ |
曲线y=-x3+3x2在点(1,2)处的切线方程为 ( ).
| A.y=3x-1 | B.y=-3x+5 |
| C.y=3x+5 | D.y=2x |