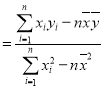题目内容
【题目】已知抛物线C:![]() , 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线.
, 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线.
(1)若抛物线C在点M的法线的斜率为![]() ,求点M的坐标
,求点M的坐标![]() ;
;
(2)设P![]() 为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P.若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P.若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,在
时,在![]() 上有三点
上有三点![]() ,
,![]() 及
及![]() ,在该点的法线通过点
,在该点的法线通过点![]() ,法线方程分别为
,法线方程分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,在
时,在![]() 上有一点
上有一点![]() ,在该点的法线通过点
,在该点的法线通过点![]() ,法线方程为
,法线方程为![]() .
.
【解析】
试题分析:(1)求导可得点![]() 处切线的斜率
处切线的斜率![]()
![]() 法线斜率为
法线斜率为![]()
![]()
![]() =
=![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ;(2)设
;(2)设![]()
![]() 为
为![]() 上一点,由
上一点,由![]()
![]()
![]() 上点
上点![]() 处的切线斜率
处的切线斜率![]() ,
,![]() 法线方程为
法线方程为![]()
![]() 法线过点
法线过点![]()
![]() ;若
;若![]()
![]()
![]() 的法线方程为:
的法线方程为:![]()
![]()
![]()
![]()
![]() .再讨论
.再讨论![]() 和
和![]() ,即可求得:当
,即可求得:当![]() 时,有三点和三条法线;当
时,有三点和三条法线;当![]() 时,有一点和一条法线.
时,有一点和一条法线.
试题解析:(1)函数![]() 的导数
的导数![]() ,点
,点![]() 处切线的斜率
处切线的斜率![]()
![]() 过点
过点![]() 的法线斜率为
的法线斜率为![]()
![]()
![]() =
=![]() ,解得
,解得![]() ,
,![]() 。故点
。故点![]() 的坐标为
的坐标为![]() 。
。
(2)设![]()
![]() 为
为![]() 上一点,
上一点,
若![]() ,则
,则![]() 上点
上点![]() 处的切线斜率
处的切线斜率![]() ,过点
,过点![]() 的法线方程为
的法线方程为![]() , 法线过点
, 法线过点![]()
![]() ;
;
若![]() ,则过点
,则过点![]()
![]() 的法线方程为:
的法线方程为:![]() 。
。
若法线过点![]()
![]() ,则
,则![]() ,即
,即![]() 。
。
若![]() ,则
,则![]() ,从而
,从而![]() ,
,
代入得![]() ,
,![]() 。
。
若![]() ,与
,与![]() 矛盾,若
矛盾,若![]() ,则无解。
,则无解。
综上,当![]() 时,在
时,在![]() 上有三点
上有三点![]() ,
,![]() 及
及![]() ,在该点的法线通过点
,在该点的法线通过点![]() ,法线方程分别为
,法线方程分别为![]() ,
,![]() ,
,![]() 。
。
当![]() 时,在
时,在![]() 上有一点
上有一点![]() ,在该点的法线通过点
,在该点的法线通过点![]() ,法线方程为
,法线方程为![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目