题目内容
【题目】已知椭圆![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设![]() 为坐标原点,
为坐标原点,![]() 为椭圆
为椭圆![]() 上的三个动点,若四边形
上的三个动点,若四边形![]() 为平行四边形,判断
为平行四边形,判断![]() 的面积是否为定值,并说明理由.
的面积是否为定值,并说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 的面积为定值
的面积为定值![]() .
.
【解析】
试题分析:(Ⅰ)由已知,椭圆![]() 的标准方程为
的标准方程为![]() ,则离心率
,则离心率![]() ;(Ⅱ)由已知,
;(Ⅱ)由已知,![]() 的面积等于
的面积等于![]() 的面积,分情况:若
的面积,分情况:若![]() 是椭圆的右顶点,
是椭圆的右顶点,![]() 的面积
的面积![]() ;若
;若![]() 不是椭圆的左、右顶点,可设
不是椭圆的左、右顶点,可设![]() ,
,![]() ,则由四边形
,则由四边形![]() 为平行四边形,得
为平行四边形,得![]() ,即
,即![]() ,联立方程由韦达定理知
,联立方程由韦达定理知![]()
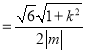 ,又
,又![]() 到
到![]() 的距离
的距离![]() ,所以
,所以![]() 的面积
的面积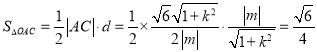 .
.
试题解析:(Ⅰ)椭圆![]() 的标准方程为:
的标准方程为:![]()
所以![]() 。
。
所以椭圆![]() 的离心率
的离心率![]() 。
。
(Ⅱ)①若![]() 是椭圆的右顶点(左顶点一样),此时
是椭圆的右顶点(左顶点一样),此时![]() 垂直平方
垂直平方![]() 。
。
所以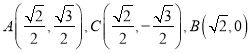 。
。
![]()
所以![]() 的面积
的面积![]() 。
。
②若![]() 不是椭圆的左、右顶点,设
不是椭圆的左、右顶点,设![]() ,
,
![]() ,
,
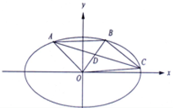
由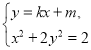 得
得![]() ,
,
![]() ,
,
![]() 。
。
因为四边形![]() 为平行四边形,
为平行四边形,
所以![]() 。
。
所以![]() ,
,
代入椭圆方程,化简得![]() 。
。
因为![]()
![]()
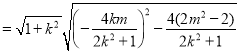
![]()
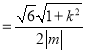 。
。
点![]() 到
到![]() 的距离
的距离![]() 。
。
所以![]() 的面积
的面积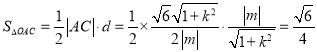 。
。
综上,![]() 的面积为定值
的面积为定值![]() 。
。
因为![]() 的面积等于
的面积等于![]() 的面积,
的面积,
所以![]() 的面积为定值
的面积为定值![]() 。
。

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
