题目内容
已知点P是椭圆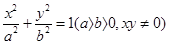 上的动点,
上的动点,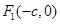 、
、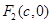 为椭圆的左、右焦点,O为坐标原点,若M是
为椭圆的左、右焦点,O为坐标原点,若M是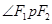 的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
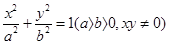 上的动点,
上的动点,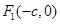 、
、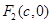 为椭圆的左、右焦点,O为坐标原点,若M是
为椭圆的左、右焦点,O为坐标原点,若M是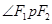 的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( ) A.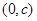 | B.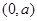 | C.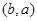 | D.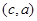 |
A
解:如图,延长PF2,F1M,交与N点,∵PM是∠F1PF2平分线,且F1M⊥MP,
∴|PN|=|PF1|,M为F1F2中点,
连接OM,∵O为F1F2中点,M为F1F2中点
∴|OM|=
 |F2N|=
|F2N|= ||PN|﹣|PF2||=
||PN|﹣|PF2||= ||PF1|﹣|PF2||
||PF1|﹣|PF2||∵在椭圆
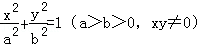 中,设P点坐标为(x0,y0)
中,设P点坐标为(x0,y0)则|PF1|=a+ex0,|PF2|=a﹣ex0,
∴||PF1|﹣|PF2||=|a+ex0+a﹣ex0|=|2ex0|=|x0|
∵P点在椭圆
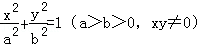 上,
上,∴|x0|∈(0,a],
又∵当|x0|=a时,F1M⊥MP不成立,∴|x0|∈(0,a)
∴|OM|∈(0,c).
故选A.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的方程为
的方程为 ,斜率为1的直线
,斜率为1的直线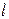 与椭圆
与椭圆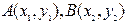 两点.
两点. ,直线
,直线 过点
过点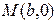 ,且
,且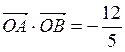 ,求椭圆
,求椭圆 的方程;
的方程; ,若点
,若点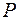 在椭圆
在椭圆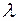 的取值范围.
的取值范围. 上一点,
上一点,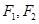 分别是左、右焦点,若
分别是左、右焦点,若 ,则
,则
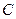 :
: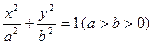 的离心率为
的离心率为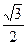 ,过坐标原点
,过坐标原点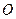 且斜率为
且斜率为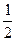 的直线
的直线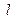 与
与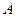 、
、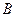 ,
,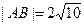 .
.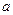 、
、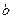 的值;
的值;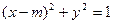 与椭圆
与椭圆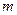 的取值范围.
的取值范围.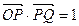 .
.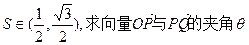 的取值范围;
的取值范围;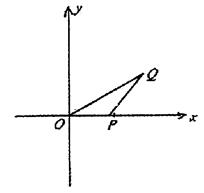
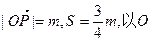 为中心,P为焦点的椭圆经过点Q,当m≥2时,求
为中心,P为焦点的椭圆经过点Q,当m≥2时,求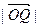 的最小值,并求出此时的椭圆方程。
的最小值,并求出此时的椭圆方程。 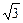 ),椭圆
),椭圆 +
+ 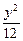 =1的右焦点为F,点P在椭圆上移动,当|PA|+2|PF|取最小值时,P点的坐标是__________.
=1的右焦点为F,点P在椭圆上移动,当|PA|+2|PF|取最小值时,P点的坐标是__________. 上两点间最大的距离为8,则实数
上两点间最大的距离为8,则实数 的值是 ▲
的值是 ▲  的右准线上,过P点且方向向量为
的右准线上,过P点且方向向量为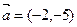 的光线经直线y=-2反射后通过椭圆的右焦点,则这个椭圆的离心率为 .
的光线经直线y=-2反射后通过椭圆的右焦点,则这个椭圆的离心率为 .