题目内容
8.(1)求证:$A_9^9-9A_8^8+8A_7^7=A_8^8$(2)求${({2{x^3}-\frac{1}{{4{x^3}}}})^{10}}$的展开式的常数项.
(3)求(1+x+x2)(1+x)10的展开式中x4的系数.
分析 (1)利用阶乘公式,即可证明;
(2)根据题意${({2{x^3}-\frac{1}{{4{x^3}}}})^{10}}$的展开式通项为Tr+1=C10r(2x3)10-r(-$\frac{1}{4{x}^{3}}$)r=C10r•210-r•(-4)-r(x)30-6r,
令x的指数为0,可得r的值,即可得其展开式中的常数项为第6项,将r=5代入通项可得T6,即可得答案;
(3)在(1+x+x2)(1+x)10的展开式中,含x4项是1×C104x4+x•C103x3+x2•C102x2,由此能求出其系数.
解答 (1)证明:左边=9!-9•8!+8•7!=9!-9!+8!=${A}_{8}^{8}$=右边,
∴$A_9^9-9A_8^8+8A_7^7=A_8^8$;
(2)解:根据题意${({2{x^3}-\frac{1}{{4{x^3}}}})^{10}}$的展开式通项为Tr+1=C10r(2x3)10-r(-$\frac{1}{4{x}^{3}}$)r=C10r•210-r•(-4)-r(x)30-6r,
令30-6r=0,可得r=5,即其展开式中的常数项为第6项,
则T6=-$\frac{63}{8}$,即其展开式中的常数项为-$\frac{63}{8}$;
(3)解:1×C104x4+x•C103x3+x2•C102x2
=210x4+120x4+45x4
=375x4.
∴在(1+x+x2)(1+x)10的展开式中,含x4项的系数是375.
点评 本题考查二项式系数的性质,考查二项式定理的应用,解题的关键要正确写出并化简该二项式展开式的通项.

练习册系列答案
相关题目
2.由1、2、3、4、5、6组成没有重复数字且1、3、5互不相邻的六位偶数的个数是( )
| A. | 108 | B. | 72 | C. | 48 | D. | 36 |
3.已知函数y=x3-3x+c的图象与x轴恰好2个交点,则c=( )
| A. | -3或1 | B. | -9或3 | C. | -1或1 | D. | -2或2 |
20.已知(3x-1)n=a0+a1x+a2x2+a3x3+…+anxn(n∈N*),设(3x-1)n展开式的二项式系数和为Sn,Tn=a1+a2+a3+…+an(n∈N*),Sn与Tn的大小关系是( )
| A. | Sn>Tn | |
| B. | Sn<Tn | |
| C. | n为奇数时,Sn<Tn,n为偶数时,Sn>Tn | |
| D. | Sn=Tn |
20.已知向量$\overrightarrow a=(6,2)$,向量$\overrightarrow b=(x,3)$,且$\overrightarrow a$∥$\overrightarrow b$,则x=( )
| A. | 1 | B. | 5 | C. | 9 | D. | 10 |
18.将389(10)化成五进位制数的末位是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
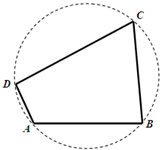 如图,我国南海某处的一个圆形海域上有四个小岛,小岛B与小岛A、小岛C相距都为5n mile,与小岛D相距为$3\sqrt{5}$n mile.小岛A对小岛B与D的视角为钝角,且$sinA=\frac{3}{5}$.
如图,我国南海某处的一个圆形海域上有四个小岛,小岛B与小岛A、小岛C相距都为5n mile,与小岛D相距为$3\sqrt{5}$n mile.小岛A对小岛B与D的视角为钝角,且$sinA=\frac{3}{5}$.