题目内容
20.已知向量$\overrightarrow a=(6,2)$,向量$\overrightarrow b=(x,3)$,且$\overrightarrow a$∥$\overrightarrow b$,则x=( )| A. | 1 | B. | 5 | C. | 9 | D. | 10 |
分析 根据向量平行的坐标公式进行求解即可.
解答 解:若$\overrightarrow a$∥$\overrightarrow b$,
则6×3-2x=0,
解得x=9.
故选:C.
点评 本题主要考查向量平行的坐标公式的应用,比较基础.

练习册系列答案
相关题目
14.设F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两个焦点,P在双曲线上,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,$|{\overrightarrow{P{F_1}}}|•|{\overrightarrow{P{F_2}}}|=2ac$(c为半焦距),则双曲线的离心率为( )
| A. | $\frac{{\sqrt{3}-1}}{2}$ | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | 2 | D. | $\frac{{\sqrt{5}+1}}{2}$ |
15.已知x,y的取值如表所示:若y与x呈线性相关,且回归方程为$\widehat{y}$=$\widehat{b}$x+$\frac{7}{2}$,则$\widehat{b}$等于0.5
| x | 2 | 3 | 4 |
| y | 5 | 4 | 6 |
12.如图所示的算法流程图运行后,输出结果是( )
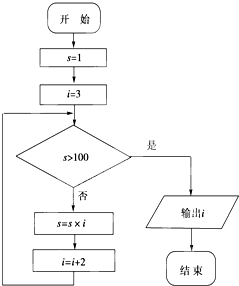

| A. | 7 | B. | 8 | C. | 9 | D. | 11 |