题目内容

3．已知复数z=2-i，则|z|=$\sqrt{5}$．

分析 根据复数模长的定义直接进行计算即可．

解答 解：∵复数z=2-i，
∴|z|=$\sqrt{4+1}$=$\sqrt{5}$．
故答案为：$\sqrt{5}$．

点评 本题主要考查复数的长度的计算，比较基础．

练习册系列答案
相关题目
17．化简2$\sqrt{1+sin10}$+$\sqrt{2+2cos10}$的结果是（　　）
A．2sin5B．4cos5+2sin5C．-4cos5-2sin5D．-2sin5
18．已知函数f（x）=tanx-sinx，下列命题中正确的是②③（写出所有正确命题的序号）
①f（x）的周期为π；              ②f（x）的图象关于点（π，0）对称；
③f（x）在（$\frac{π}{2}，π$）上单调递增；   ④f（x）在（-$\frac{π}{2}$，$\frac{π}{2}$）上有3个零点．
15．已知x，y的取值如表所示：若y与x呈线性相关，且回归方程为$\widehat{y}$=$\widehat{b}$x+$\frac{7}{2}$，则$\widehat{b}$等于0.5
x234
y546
2．已知平面α，β和直线a，b，若α∩β=l，a?α，b?β，且平面与平面β不垂直，直线a与直线l不垂直，直线b与直线l不垂直，则（　　）
A．直线a与直线b可能垂直，但不可能平行
B．直线a与直线b可能垂直，也可能平行
C．直线a与直线b不可能垂直，但可能平行
D．直线a与直线b不可能垂直，也不可能平行
8．（1）求证：$A_9^9-9A_8^8+8A_7^7=A_8^8$
（2）求${（{2{x^3}-\frac{1}{{4{x^3}}}}）^{10}}$的展开式的常数项．
（3）求（1+x+x2）（1+x）10的展开式中x4的系数．
15．已知α是第二象限的角，且$sinα=\frac{3}{5}$，则tan2α的值是-$\frac{24}{7}$．
12．如图所示的算法流程图运行后，输出结果是（　　） 
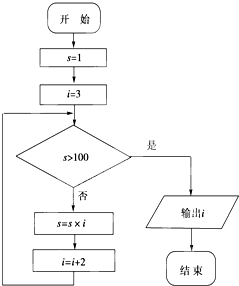
A．7B．8C．9D．11
13．设f（x）、g（x）分别是定义在R上的奇函数和偶函数，当x＜0时，f′（x）•g（x）+f（x）•g′（x）＞0，且f（-3）•g（-3）=0，则不等式f（x）•g（x）＜0的解集是（　　）
A．（-3，0）∪（3，+∞）B．（-3，0）∪（0，3）C．（-∞，-3）∪（3，+∞）D．（-∞，-3）∪（0，3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网