题目内容
(本小题满分12分)
设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程 有实数根;②函数
有实数根;②函数 ”
”
(I)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意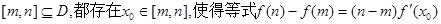 成立。试用这一性质证明:方程
成立。试用这一性质证明:方程 只有一个实数根;
只有一个实数根;
(III)对于M中的函数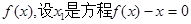 的实数根,求证:对于
的实数根,求证:对于 定义域中任意的
定义域中任意的 当
当 且
且
设M是由满足下列条件的函数
 构成的集合:“①方程
构成的集合:“①方程 有实数根;②函数
有实数根;②函数 ”
”(I)判断函数
 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;(II)集合M中的元素
 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意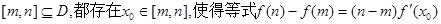 成立。试用这一性质证明:方程
成立。试用这一性质证明:方程 只有一个实数根;
只有一个实数根;(III)对于M中的函数
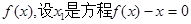 的实数根,求证:对于
的实数根,求证:对于 定义域中任意的
定义域中任意的 当
当 且
且
(1)因为
所以
又因为当 ,所以方程
,所以方程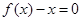 有实数根0,
有实数根0,
所以函数 是集合M中的元素。 …………4分
是集合M中的元素。 …………4分
(2)假设方程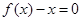 存在两个实数根
存在两个实数根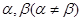 ,
,
则 …………5分
…………5分
不妨设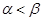 ,根据题意存在数
,根据题意存在数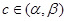 ,
,
使得等式 成立, …………7分
成立, …………7分
因为
与已知 只有一个实数根;
只有一个实数根;
…………9分
(3)不妨设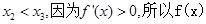 为增函数,
为增函数,
所以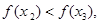
又因为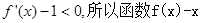 为减函数, …………10分
为减函数, …………10分
所以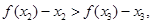 …………11分
…………11分
所以 ,
,
即
所以
…………12分

所以

又因为当
 ,所以方程
,所以方程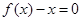 有实数根0,
有实数根0,所以函数
 是集合M中的元素。 …………4分
是集合M中的元素。 …………4分(2)假设方程
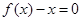 存在两个实数根
存在两个实数根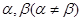 ,
,则
 …………5分
…………5分不妨设
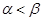 ,根据题意存在数
,根据题意存在数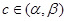 ,
,使得等式
 成立, …………7分
成立, …………7分因为

与已知
 只有一个实数根;
只有一个实数根;…………9分
(3)不妨设
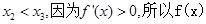 为增函数,
为增函数,所以
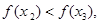
又因为
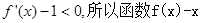 为减函数, …………10分
为减函数, …………10分所以
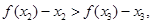 …………11分
…………11分所以
 ,
,即

所以

…………12分
略

练习册系列答案
相关题目
 在
在 上是增函数,则实数
上是增函数,则实数 的取值范围是
的取值范围是 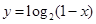


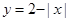
 对任意实数
对任意实数 均有
均有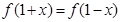 成立,且
成立,且 ,则
,则 与
与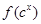 的大小关系为 ( )
的大小关系为 ( )

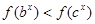
 ,函数
,函数 ,称方程
,称方程
 的取值范围;
的取值范围; ,求
,求 是定义在R上的偶函数,且在(-∞,0)上是增函数,则
是定义在R上的偶函数,且在(-∞,0)上是增函数,则 与
与
 的大小关系是( )
的大小关系是( )



 ,
, ,对于任意的
,对于任意的 都能找到
都能找到 ,使得
,使得 ,则实数
,则实数 的取值范围是 .
的取值范围是 . 对一切
对一切 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .