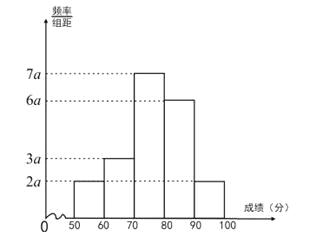
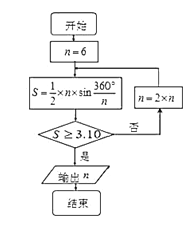
题目内容
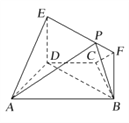
【题目】在三棱锥ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1⊥底面ABC,AA1= ![]() ,P、Q分别是AB、AC上的点,且PQ∥BC.
,P、Q分别是AB、AC上的点,且PQ∥BC. 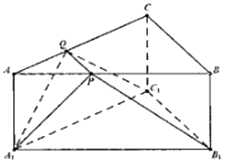
(1)若平面A1PQ与平面A1B1C1相交于直线l,求证:l∥B1C1;
(2)当平面A1PQ⊥平面PQC1B1时,确定点P的位置并说明理由.S.
【答案】
(1)证明:∵PQ∥BC∥B1C1,B1C1面A1B1C1,PQ面 A1B1C1,
∴PQ∥面A1B1C1;
∵面A1PQ∩面A1B1C1=l,∴PQ∥l,
∴l∥B1C1;
(2)证明:P为AB的中点时,平面A1PQ⊥面PQC1B1;
证明如下:作PQ的中点M,B1C1的中点N,连接A1M,MN,A1N,
∵PQ∥BC,AP=AQ,进而A1Q=A1P,∴A1M⊥PQ,
∵平面A1PQ⊥面PQC1B1,平面A1PQ∩面PQC1B1=PQ,
∴A1M⊥面PQC1B1,而MN面PQC1B1,
∴A1M⊥MN,即△A1MN为直角三角形;
连接AM并延长交BC于G,显然G是BC的中点,
设AP=x,则PB=2﹣x,则由 ![]() =
= ![]() ,可得
,可得 ![]() =
= ![]() ,解得AM=
,解得AM= ![]() x,
x,
在Rt△AA1M中, ![]() =
= ![]() +AM2=
+AM2= ![]() +
+ ![]() x2.
x2.
同理MG=AG﹣AM= ![]() ﹣
﹣ ![]() x,
x,
在Rt△MGN中,MN2=MG2+GN2= ![]() +
+ ![]() =
= ![]() ﹣3x+
﹣3x+ ![]() x2.
x2.
∴在Rt△A1MN中, ![]() =
= ![]() +MN2,
+MN2,
即3= ![]() +
+ ![]() x2+
x2+ ![]() ﹣3x+
﹣3x+
解得x=1,即AP=1,此时P为AB的中点
【解析】(1)利用线面平行的性质证明l∥B1C1;(2)作PQ的中点M,B1C1的中点N,连接A1M,MN,A1N,利用线面垂直的判定证明A1M⊥PQ,A1M⊥MN,即可平面A1PQ⊥面PQB1C1 , 再利用余弦定理即可确定P点的位置.
【考点精析】通过灵活运用平面的基本性质及推论和平面与平面垂直的性质,掌握如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线;两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直即可以解答此题.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案