题目内容
16.将函数y=sin(x+$\frac{π}{6}$)的图象上各点的横坐标压缩为原来的$\frac{1}{2}$倍(纵坐标不变),所得函数在下面哪个区间单调递增( )| A. | (-$\frac{π}{3}$,$\frac{π}{6}$)? | B. | (-$\frac{π}{2}$,$\frac{π}{2}$)? | C. | (-$\frac{π}{3}$,$\frac{π}{3}$)?? | D. | (-$\frac{π}{6}$,$\frac{2π}{3}$)? |
分析 利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的增区间,求得y=g(x)的单调递增区间.
解答 解:将函数y=sin(x+$\frac{π}{6}$)图象上每一点的横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),得到函数y=sin(2x+$\frac{π}{6}$)的图象;
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,
可得函数g(x)的增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈z,
当k=0时,可得函数在区间(-$\frac{π}{3}$,$\frac{π}{6}$)单调递增.
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的增区间,属于基础题.

练习册系列答案
相关题目
6.如图,在棱长为3的正方体ABCD-A1B1C1D1中,点C1到平面A1BD的距离为( )
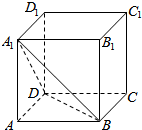

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
11.已知数列{an}中,a2=102,an+1-an=4n,则数列$\left\{{\frac{a_n}{n}}\right\}$的最小项是( )
| A. | 第6项 | B. | 第7项 | C. | 第8项 | D. | 第9项 |
5.方程|x|+|y|=1表示的曲线是( )
| A. |  | B. | 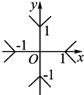 | C. | 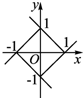 | D. | 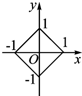 |
6.命题p:?x>0,总有x2-1≥0,则?p为( )
| A. | ?x0≤0,使得x2-1<0 | B. | ?x0>0,使得x2-1<0 | ||
| C. | ?x>0,总有x2-1<0 | D. | ?x≤0,总有x2-1<0 |
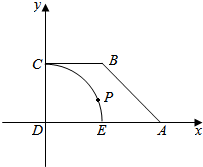 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.