Question

2．已知函数f（x）=ln（x+$\frac{1}{a}$）-ax，其中a＞0．
（1）a=1时，试讨论f（x）的单调性；
（2）若存在实数x₁、x₂满足-$\frac{1}{a}$＜x₁＜0，x₂＞0，且f（x₁）=f（x₂）=0，求证：x₁+x₂＞0．

Answer 1

分析 （1）求出当a=1的f（x）的导数，令导数大于0，得增区间，令导数小于0，得减区间；
（2）求出f（x）的导数，求得增区间和减区间，进而得到最大值，令最大值大于0，可得0＜a＜1，讨论a的变化，结合图象即可得证．

解答 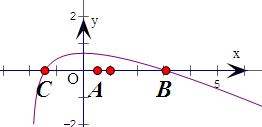（1）解：当a=1时，f（x）=ln（x+1）-x，
f′（x）=$\frac{1}{x+1}$-1=$\frac{-x}{x+1}$，
当-1＜x＜0时，f′（x）＞0，f（x）递增；
当x＞0时，f′（x）＜0，f（x）递减．
则有f（x）在（-1，0）递增，在（0，+∞）递减；
（2）证明：函数f（x）=ln（x+$\frac{1}{a}$）-ax的导数为
f′（x）=$\frac{1}{x+\frac{1}{a}}$-a=$\frac{-ax}{x+\frac{1}{a}}$，
当-$\frac{1}{a}$＜x＜0时，f′（x）＞0，f（x）递增；
当x＞0时，f′（x）＜0，f（x）递减．
即有x=0处f（x）取得极大值，也为最大值ln$\frac{1}{a}$=-lna，
由题意可得当-lna＞0，即0＜a＜1，f（x）=0有两个实根x₁，x₂，
且-$\frac{1}{a}$＜x₁＜0，x₂＞0，
讨论a→1时，由（1）可得，f（x）与x轴的交点越来越趋向于原点，x₁+x₂→0；
当a→0时，可得f（x）与x轴的两交点越来越远离原点，且右边的交点变化得快，
则有x₁+x₂＞0．

点评 本题考查导数的运用：求单调区间、极值和最值，考查方程和函数的零点的关系，运用数形结合的思想方法是解题的关键．