题目内容
13.已知关于x的不等式|xlnx|≤-2x2+cx-$\frac{1}{2}$有解,则正整数c的最小值为3.分析 由于x>0,则原不等式即为|lnx|+2x+$\frac{1}{2x}$≤c,令f(x)=|lnx|+2x+$\frac{1}{2x}$,讨论x≥1,x<1去绝对值,运用导数判断单调性,即可求得最小值,再由c为正整数,即可得到最小值c=3.
解答 解:由于x>0,则不等式|xlnx|≤-2x2+cx-$\frac{1}{2}$即为
|lnx|+2x+$\frac{1}{2x}$≤c,
令f(x)=|lnx|+2x+$\frac{1}{2x}$,
当x≥1时,f(x)=lnx+$\frac{1}{2x}$+2x,
由于f′(x)=$\frac{1}{x}$+2-$\frac{1}{2{x}^{2}}$>0,
则f(x)在[1,+∞)递增,
则有f(1)为最小值$\frac{5}{2}$;
当0<x<1时,f(x)=-lnx+2x+$\frac{1}{2x}$,
由于f′(x)=-$\frac{1}{x}$+2-$\frac{1}{2{x}^{2}}$=$\frac{4{x}^{2}-2x-1}{2{x}^{2}}$,
令f(x)=0,解得x=$\frac{1+\sqrt{5}}{4}$($\frac{1-\sqrt{5}}{4}$舍去),
当0<x<$\frac{1+\sqrt{5}}{4}$时,f′(x)<0,f(x)递减;
当x>$\frac{1+\sqrt{5}}{4}$时,f′(x)>0,f(x)递增.
则有x=$\frac{1+\sqrt{5}}{4}$处f(x)取得极小值,也为最小值,
由于2<-ln$\frac{1+\sqrt{5}}{4}$+$\sqrt{5}$<3,且c为正整数,即有c≥3,
则正整数c的最小值为3.
故答案为:3.
点评 本题考查不等式有解的条件,主要考查参数分离和函数的最值的求法,属于中档题和易错题.

 高效智能课时作业系列答案
高效智能课时作业系列答案| A. | $[{\frac{1}{2},1}]$ | B. | $[{\frac{3}{4},1}]$ | C. | $[{\frac{1}{2},\frac{3}{4}}]$ | D. | $[{\frac{3}{8},\frac{3}{4}}]$ |
 某市为了节约能源,拟出台“阶梯电价”制度,即制定住户月用电量的临界值a,若某住户某月用电量不超过a度,则按平价计费;若某月用电量超过a度,则超出部分按议价计费.未超出分布按平价计费.为确定a的值,随机调查了该市100户的月用电量,工作人员已将90户的用电量填在了下面的频率分布表中,最后10户的月用电量(单位:度)为:18 63 43 119 65 77 29 97 52 100
某市为了节约能源,拟出台“阶梯电价”制度,即制定住户月用电量的临界值a,若某住户某月用电量不超过a度,则按平价计费;若某月用电量超过a度,则超出部分按议价计费.未超出分布按平价计费.为确定a的值,随机调查了该市100户的月用电量,工作人员已将90户的用电量填在了下面的频率分布表中,最后10户的月用电量(单位:度)为:18 63 43 119 65 77 29 97 52 100| 组别 | 月用电量 | 频数统计 | 频数 | 频率 |
| 1 | [0,20) |  | ||
| 2 | [20,40) | 正正一 | ||
| 3 | [40,60) | 正正正正 | ||
| 4 | [60,80) | 正正正正正 | ||
| 5 | [80,100) | 正正正正 | ||
| 6 | [100,120) |  |
(Ⅱ)根据已有信息,试估计全市住户的平均用电量(同一组数据用该区间的中点值作代表);
(Ⅲ)若该市计划让全市75%的住户在“阶梯电价”出台前后缴纳的电费不变,试求临界值a.
 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱DD1、C1D1的中点. 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PCD⊥底面ABCD(1)若M,N分别为PC,BD的中点,求证:MN∥平面PAD;
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PCD⊥底面ABCD(1)若M,N分别为PC,BD的中点,求证:MN∥平面PAD;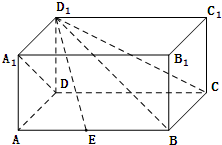 在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1.
在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1.