题目内容
【题目】若圆![]() 的内接矩形的周长最大值为
的内接矩形的周长最大值为![]() .
.

(1)求圆O的方程;
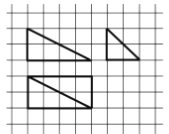
(2)若过点![]() 的直线
的直线![]() 与圆O交于A,B两点,如图所示,且直线
与圆O交于A,B两点,如图所示,且直线![]() 的斜率
的斜率![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)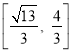
【解析】
(1) 设矩形在第一象限点为 (x,y) (x> 0,y> 0),则![]() ,表示出矩形的周长,利用基本不等式求其最大值,根据等号的成立条件可得
,表示出矩形的周长,利用基本不等式求其最大值,根据等号的成立条件可得![]() ,进而可得圆的方程;
,进而可得圆的方程;
(2) )设直线AB:![]() ,
,![]() ,联立:
,联立: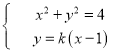 ,利用韦达定理求出
,利用韦达定理求出![]() 和
和![]() ,利用单调性求出
,利用单调性求出![]() 的取值范围.
的取值范围.
解:(1) 设矩形在第一象限点为 (x,y) (x> 0,y> 0),则![]() ,
,
∴矩形周长![]() ,
,
∵ ![]() ,
,
∴![]() ,
,
∴![]() ,
,
当且仅当 取“=”
取“=”
∴矩形周长的最大值为![]() ,
,
∴r = 2,∴圆O的方程:![]()
(2)设直线AB:![]() ,
,![]() ,
,
联立: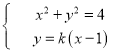 ,
,
消去y并整理得![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理:![]()
∴![]()
![]() ,
,
∵![]() ,
,
∴![]() 异号,
异号,
∴![]()
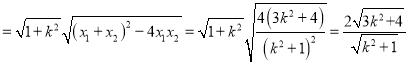
∴ ,
,
∵![]() ,
,
∴![]() ,
,
∴ .
.

练习册系列答案
相关题目