题目内容
【题目】长沙某超市计划按月订购一种冰激凌,每天进货量相同,进货成本为每桶5元,售价为每桶7元,未售出的冰激凌以每桶3元的价格当天全部处理完毕.根据往年销售经验,每天的需求量与当天最高气温(单位:![]() )有关,如果最高气温不低于
)有关,如果最高气温不低于![]() ,需求量为600桶;如果最高气温(单位:
,需求量为600桶;如果最高气温(单位:![]() )位于区间
)位于区间![]() ,需求量为400桶;如果最高气温低于
,需求量为400桶;如果最高气温低于![]() ,需求量为200桶.为了确定今年九月份的订购计划,统计了前三年九月份各天的最高气温数据,得下面的频数分布表:
,需求量为200桶.为了确定今年九月份的订购计划,统计了前三年九月份各天的最高气温数据,得下面的频数分布表:
最高气温( |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求九月份这种冰激凌一天的需求量![]() (单位:桶)的分布列;
(单位:桶)的分布列;
(2)设九月份一天销售这种冰激凌的利润为![]() (单位:元),当九月份这种冰激凌一天的进货量
(单位:元),当九月份这种冰激凌一天的进货量![]() (单位:桶)为多少时,
(单位:桶)为多少时,![]() 的均值取得最大值?
的均值取得最大值?
【答案】(1)见解析;(2)当![]() 时,
时,![]() 的数学期望
的数学期望![]() 取得最大值640。
取得最大值640。
【解析】
(1)由已知得,![]() 的可能取值为200,400,600,记六月份最高气温低于20为事件
的可能取值为200,400,600,记六月份最高气温低于20为事件![]() ,最高气温位于区间
,最高气温位于区间![]() ,
,![]() 为事件
为事件![]() ,最高气温不低于25为事件
,最高气温不低于25为事件![]() ,结合频数分布表,用频率估计概率,能求出六月份这种冰激凌一天的需求量
,结合频数分布表,用频率估计概率,能求出六月份这种冰激凌一天的需求量![]() (单位:桶)的分布列.
(单位:桶)的分布列.
(2)结合题意得当![]() 时,
时,![]() ,分别求出当
,分别求出当![]() ,
,![]() ,
,![]() 时的数学期望,由此能求出当
时的数学期望,由此能求出当![]() 时,
时,![]() 的数学期望
的数学期望![]() 取得最大值640.
取得最大值640.
(1)由已知得,![]() 的可能取值为200,400,600,记六月份最高气温低于20为事件
的可能取值为200,400,600,记六月份最高气温低于20为事件![]() ,最高气温位于区间
,最高气温位于区间![]() ,
,![]() 为事件
为事件![]() ,最高气温不低于25为事件
,最高气温不低于25为事件![]() ,
,
根据题意,结合频数分布表,用频率估计概率,
可知![]() ,
,
故六月份这种冰激凌一天的需求量![]() (单位:桶)的分布列为:
(单位:桶)的分布列为:
| 200 | 400 | 600 |
|
|
|
|
(2)结合题意得当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,
![]()
![]() ,
,
当![]() 时,
时,
![]()
![]() ,
,
所以当![]() 时,
时,![]() 的数学期望
的数学期望![]() 取得最大值640.
取得最大值640.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| n | 0.350 |
第3组 |
| 30 | p |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
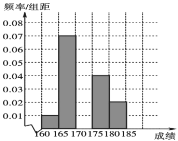
(1)求频率分布表中n,p的值,并估计该组数据的中位数(保留l位小数);
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.