题目内容
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| n | 0.350 |
第3组 |
| 30 | p |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
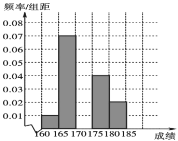
(1)求频率分布表中n,p的值,并估计该组数据的中位数(保留l位小数);
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
【答案】(1)![]() ,
,![]() ,中位数估计值为171.7(2)第3、4、5组每组各抽学生人数为3、2、1(3)
,中位数估计值为171.7(2)第3、4、5组每组各抽学生人数为3、2、1(3)![]()
【解析】
(1)由频率分布表可得:![]() ,
,![]() ,由中位数的求法可得中位数估计值为171.7;
,由中位数的求法可得中位数估计值为171.7;
(2)因为笔试成绩高的第3、4、5组的人数之比为![]() ,由分层抽样的方法选6名学生,三个小组分别选的人数为3、2、1;
,由分层抽样的方法选6名学生,三个小组分别选的人数为3、2、1;
(3)先列举出从6名学生中随机抽取2名学生的不同取法,再列举出第4组至少有1名学生被甲考官面试的取法,再结合古典概型的概率公式即可得解.
解:(1)由已知:![]() ,
,
![]() ,
,
![]() ,
,![]() ,中位数为
,中位数为![]()
![]() 171.7,
171.7,
即中位数估计值为171.7,
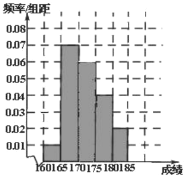
(2)由已知,笔试成绩高的第3、4、5组的人数之比为![]() ,现用分层抽样的方法选6名学生。故第3、4、5组每组各抽学生人数为3、2、1。
,现用分层抽样的方法选6名学生。故第3、4、5组每组各抽学生人数为3、2、1。
(3)在(2)的前提下,记第3组的3名学生为![]() ,
,![]() ,
,![]() ,
,
第4组的2名学生为![]() ,
,![]() ,第5组的1名学生为
,第5组的1名学生为![]() ,且“第4组至少有1名学生被甲考官面试”为事件A。
,且“第4组至少有1名学生被甲考官面试”为事件A。
则所有的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,一共15种。
,一共15种。
A事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,一共9种。
,一共9种。
![]() ,
,
答:第4组至少有1名学生被甲考官面试的概率为![]() 。
。

【题目】2018年6月14日,世界杯足球赛在俄罗斯拉开帷幕,世界杯给俄罗斯经济带来了一定的增长,某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况,随机抽查了该商品商店某天200名顾客的消费金额情况,得到如图频率分布表:将消费顾客超过4万卢布的顾客定义为”足球迷”,消费金额不超过4万卢布的顾客定义为“非足球迷”。
消费金额/万卢布 |
|
|
|
|
|
| 合计 |
顾客人数 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求这200名顾客消费金额的中位数与平均数(同一组中的消费金额用该组的中点值作代表;
(2)该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型,采用分层抽样的方法从“非足球迷”,“足球迷”中选取5人,再从这5人中随机选取3人进行问卷调查,则选取的3人中“非足球迷”人数的分布列和数学期望。
【题目】纪念币是一个国家为纪念国际或本国的政治、历史,文化等方面的重大事件、杰出人物、名胜古迹、珍稀动植物、体育赛事等而发行的法定货币.我国在 1984 年首次发行纪念币,目前已发行了 115 套纪念币,这些纪念币深受邮币爱好者的喜爱与收,2019 年发行的第 115 套纪念币“双遗产之泰山币”是目前为止发行的第一套异形币,因为这套纪念币的多种特质,更加受到爱好者追捧.某机构为调查我国公民对纪念币的喜爱态度,随机选了某城市某小区的 50 位居民调查,调查结果统计如下:
喜爱 | 不喜爱 | 合计 | |
年龄不大于40岁 | 24 | ||
年龄大于40岁 | 40 | ||
合计 | 22 | 50 |
(1)根据已有数据,把表格数据填写完整;
(2)判断能否在犯错误的概率不超过 1% 的前提下认为不同年龄与纪念币的喜爱无关?
【题目】长沙某超市计划按月订购一种冰激凌,每天进货量相同,进货成本为每桶5元,售价为每桶7元,未售出的冰激凌以每桶3元的价格当天全部处理完毕.根据往年销售经验,每天的需求量与当天最高气温(单位:![]() )有关,如果最高气温不低于
)有关,如果最高气温不低于![]() ,需求量为600桶;如果最高气温(单位:
,需求量为600桶;如果最高气温(单位:![]() )位于区间
)位于区间![]() ,需求量为400桶;如果最高气温低于
,需求量为400桶;如果最高气温低于![]() ,需求量为200桶.为了确定今年九月份的订购计划,统计了前三年九月份各天的最高气温数据,得下面的频数分布表:
,需求量为200桶.为了确定今年九月份的订购计划,统计了前三年九月份各天的最高气温数据,得下面的频数分布表:
最高气温( |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求九月份这种冰激凌一天的需求量![]() (单位:桶)的分布列;
(单位:桶)的分布列;
(2)设九月份一天销售这种冰激凌的利润为![]() (单位:元),当九月份这种冰激凌一天的进货量
(单位:元),当九月份这种冰激凌一天的进货量![]() (单位:桶)为多少时,
(单位:桶)为多少时,![]() 的均值取得最大值?
的均值取得最大值?
【题目】为考察某种药物预防疾病的效果,进行动物试验,调查了 105 个样本,统计结果为:服药的共有 55 个样本,服药但患病的仍有 10 个样本,没有服药且未患病的有 30个样本.
(1)根据所给样本数据完成 ![]() 列联表中的数据;
列联表中的数据;
(2)请问能有多大把握认为药物有效?
(参考公式:![]() 独立性检验临界值表
独立性检验临界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合计 | |
服药 | |||
没服药 | |||
合计 |