Question

【题目】设椭圆为左右焦点,为短轴端点,长轴长为4,焦距为,且,的面积为.

(Ⅰ)求椭圆的方程

(Ⅱ)设动直线椭圆有且仅有一个公共点,且与直线相交于点.试探究:在坐标平面内是否存在定点,使得以为直径的圆恒过点?若存在求出点的坐标,若不存在.请说明理由.

Answer 1

【答案】（1） （2）存在定点P(1,0)

【解析】

（Ⅰ）由椭圆长轴长为4，焦距为2c，且b＞c，△BF1F2的面积为，列方程组，求出a，b，c，得椭圆方程．（Ⅱ）将直线l方程与椭圆方程联立，由直线与椭圆有且只有一个公共点，求出M，由，得N（4，4k+m）．假设存在定点P满足条件，由图形对称性知，点P必在x轴上．设P（x1，0），由，得（4x1﹣4）+x12﹣4x1+3＝0，由此可求出满足条件的定点.

(1)由题意知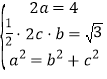，解得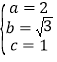：，故椭圆C的方程是．

(2)由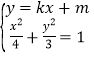得(4k2＋3)x2＋8kmx＋4m2－12＝0．

因为动直线l与椭圆C有且只有一个公共点M(x0，y0)，所以m≠0且Δ＝0，

即64k2m2－4(4k2＋3)(4m2－12)＝0，化简得4k2－m2＋3＝0.(*)

此时x0＝－＝－，y0＝kx0＋m＝，所以M(－

由得N(4,4k＋m)．

假设平面内存在定点P满足条件，由图形对称性知，点P必在x轴上．

设P(x1,0)，则对满足(*)式的m、k恒成立．

因为＝(－，＝(4－x1,4k＋m)，由，

得-＋－4x1＋x＋＋3＝0，

整理，得(4x1－4)＋x－4x1＋3＝0.(**)

由于(**)式对满足(*)式的m，k恒成立，所以解得x1＝1.

故存在定点P(1,0)，使得以MN为直径的圆恒过点M.