题目内容
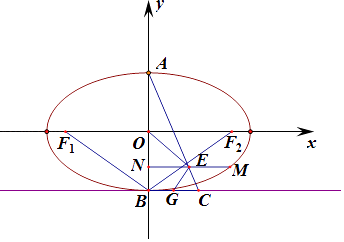
【题目】已知椭圆W: ![]() (a>b>0)的上下顶点分别为A,B,且点B(0,﹣1).F1 , F2分别为椭圆W的左、右焦点,且∠F1BF2=120°.
(a>b>0)的上下顶点分别为A,B,且点B(0,﹣1).F1 , F2分别为椭圆W的左、右焦点,且∠F1BF2=120°.
(Ⅰ)求椭圆W的标准方程;
(Ⅱ)点M是椭圆上异于A,B的任意一点,过点M作MN⊥y轴于N,E为线段MN的中点.直线AE与直线y=﹣1交于点C,G为线段BC的中点,O为坐标原点.求∠OEG的大小.
【答案】解:(Ⅰ)依题意,得b=1.又∠F1BF2=120°,
在Rt△BF1O中,∠F1BO=60°,则a=2.
∴椭圆W的标准方程为 ![]() .
.
(Ⅱ)设M(x0,y0),x0≠0,则N(0,y0),E ![]() .
.
由点M在椭圆W上,则 ![]() .即
.即 ![]() .
.
又A(0,1),则直线AE的方程为 ![]() .
.
令y=﹣1,得C ![]() .
.
又B(0,﹣1),G为线段BC的中点,则G ![]() .
.
∴ ![]() ,
, ![]() .
.
∵ ![]() =
= ![]()
= ![]() =1﹣y0﹣1+y0=0,
=1﹣y0﹣1+y0=0,
∴ ![]() .则∠OEG=90°,
.则∠OEG=90°,
∠OEG为90°.
【解析】(Ⅰ)由b=1,由∠F1BO=60°,则a=2.即可求得椭圆W的标准方程;(Ⅱ)由题意设N和E点坐标,设直线AE的方程,当y=﹣1,即可求得C点坐标,求得G点坐标,则 ![]() ,
, ![]() .根据向量数量积的坐标运算,即可求得
.根据向量数量积的坐标运算,即可求得 ![]()
![]() =0,则
=0,则 ![]() ,则∠OEG=90°.
,则∠OEG=90°.

练习册系列答案
相关题目