题目内容
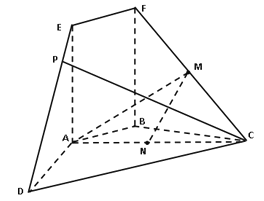
【题目】已知矩形![]() 为
为![]() 中点,沿直线
中点,沿直线![]() 将
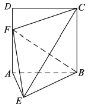
将![]() 翻折成
翻折成![]() ,直线
,直线![]() 与平面
与平面![]() 所成角最大时,线段
所成角最大时,线段![]() 长是( )
长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
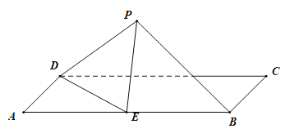
取![]() 的中点
的中点![]() ,连接
,连接![]() 交于
交于![]() 的中点
的中点![]() ,
,![]() ,进而有
,进而有![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,可证
,可证![]() 平面
平面![]() ,连接
,连接![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,平面
,平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,根据条件可知
,根据条件可知![]() ,
,![]() 平面
平面![]() ,
,![]() ,通过边长关系求出
,通过边长关系求出![]() ,
,![]() ,
,![]() ,以及利用余弦定理求出
,以及利用余弦定理求出![]() ,从而得出
,从而得出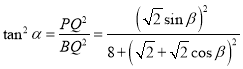 ,根据同角三角函数关系和换元法令
,根据同角三角函数关系和换元法令![]() ,得出
,得出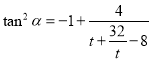 ,再根据基本不等式时得出当
,再根据基本不等式时得出当![]() 时,
时,![]() 取得最大值,从而可求出线段
取得最大值,从而可求出线段![]() 长
长
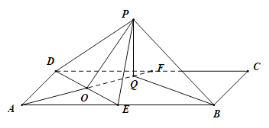
解:取![]() 的中点
的中点![]() ,连接
,连接![]() 交于
交于![]() 的中点
的中点![]() ,
,
在矩形![]() 中,
中,![]() 为
为![]() 中点,
中点,
所以四边形![]() 为正方形,
为正方形,![]() ,
,
所以![]() ,
,
故![]() 平面
平面![]() ,在平面
,在平面![]() 内过点
内过点![]() 作
作![]() 于点
于点![]() ,
,
则![]() ,所以
,所以![]() 平面
平面![]() ,连接
,连接![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,即
,即![]()
设平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以在![]() 中,
中,![]() ,
,
则![]() ,
,
在![]() 中,
中,![]() ,
,
则由余弦定理得出:![]() ,
,
则有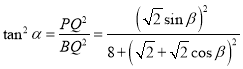
![]()
![]()
![]()
![]() ,
,
令![]() ,则
,则![]() ,
,
即: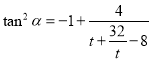 ,
,
当直线![]() 与平面
与平面![]() 所成角
所成角![]() 最大时,
最大时,![]() 最大,
最大,
即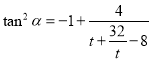 取得最大值时,当且仅当
取得最大值时,当且仅当![]() ,
,
此时![]() ,
,
所以,![]()
![]() ,
,
即![]() .
.
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目