题目内容
【题目】已知
，
分别是双曲线
的左顶点、右焦点，过的直线
与
的一条渐近线垂直且与另一条渐近线和
轴分别交于
，
两点.若
，则的离心率是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
由已知条件设出直线l的方程，与y＝﹣
x联立，求P点坐标，将x＝0带入直线l，求Q点坐标，由AP⊥AQ，知kAPkAQ，由此求离心率．
∵A，F分别是双曲线
的左顶点、右焦点，
∴A（﹣a，0）F（c，0），
∵过F的直线l与C的一条渐近线垂直，
且与另一条渐近线和y轴分别交于P，Q两点，
∴直线l的方程为：y＝﹣
，
直线l：y＝﹣与y＝﹣x联立：
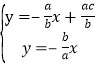，解得P点
将x＝0带入直线l：y＝﹣，得Q（0，
），
∵AP⊥AQ，∴kAPkAQ＝
×
＝﹣1，
化简得b2﹣ac﹣a2＝﹣c2，
把b2＝c2﹣a2代入，得2c2﹣2a2﹣ac＝0
同除a2得2e2﹣2﹣e＝0，
∴e＝
，或e＝
（舍）．
故选：D．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】某高中三年级的甲、乙两个同学同时参加某大学的自主招生，在申请的材料中提交了某学科10次的考试成绩，记录如下：
甲：78 86 95 97 88 82 76 89 92 95
乙：73 83 69 82 93 86 79 75 84 99
（1）根据两组数据，作出两人成绩的茎叶图，并通过茎叶图比较两人本学科成绩平均值的大小关系及方差的大小关系（不要求计算具体值，直接写出结论即可）
（2）现将两人的名次分为三个等级：
成绩分数 |
|
|
|
等级 | 合格 | 良好 | 优秀 |
根据所给数据，从甲、乙获得“优秀”的成绩组合中随机选取一组，求选中甲同学成绩高于乙同学成绩的组合的概率.
