ЬтФПФкШн
ЁОЬтФПЁПНќФъРДЃЌЙВЯэЕЅГЕвбОЧФШЛНјШыСЫЙуДѓЪаУёЕФШеГЃЩњЛюЃЌВЂТ§Т§ИФБфСЫШЫУЧЕФГіааЗНЪН.ЮЊСЫИќКУЕиЗўЮёУёжкЃЌФГЙВЯэЕЅГЕЙЋЫОдкЦфЙйЗН![]() жаЩшжУСЫгУЛЇЦРМлЗДРЁЯЕЭГЃЌвдСЫНтгУЛЇЖдГЕСОзДПіКЭгХЛнЛюЖЏЕФЦРМлЃЌЯжДгЦРМлЯЕЭГжабЁГі
жаЩшжУСЫгУЛЇЦРМлЗДРЁЯЕЭГЃЌвдСЫНтгУЛЇЖдГЕСОзДПіКЭгХЛнЛюЖЏЕФЦРМлЃЌЯжДгЦРМлЯЕЭГжабЁГі![]() ЬѕНЯЮЊЯъЯИЕФЦРМлаХЯЂНјааЭГМЦЃЌГЕСОзДПіКЭгХЛнЛюЖЏЦРМлЕФ
ЬѕНЯЮЊЯъЯИЕФЦРМлаХЯЂНјааЭГМЦЃЌГЕСОзДПіКЭгХЛнЛюЖЏЦРМлЕФ![]() СаСЊБэШчЯТ:
СаСЊБэШчЯТ:
ЖдгХЛнЛюЖЏКУЦР | ЖдгХЛнЛюЖЏВЛТњвт | КЯМЦ | |
ЖдГЕСОзДПіКУЦР |
|
|
|
ЖдГЕСОзДПіВЛТњвт |
|
|
|
КЯМЦ |
|
|
|
(1)ФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТШЯЮЊгХЛнЛюЖЏКУЦРгыГЕСОзДПіКУЦРжЎМфгаЙиЯЕ?
ЕФЧАЬсЯТШЯЮЊгХЛнЛюЖЏКУЦРгыГЕСОзДПіКУЦРжЎМфгаЙиЯЕ?
(2)ЮЊСЫЛиРЁгУЛЇЃЌЙЋЫОЭЈЙ§![]() ЯђгУЛЇЫцЛњХЩЫЭУПеХЕФУцЖюЮЊ
ЯђгУЛЇЫцЛњХЩЫЭУПеХЕФУцЖюЮЊ![]() дЊЃЌ
дЊЃЌ![]() дЊЃЌ
дЊЃЌ![]() дЊЕФШ§жжЦяааШЏЃЌгУЛЇУПДЮЪЙгУ
дЊЕФШ§жжЦяааШЏЃЌгУЛЇУПДЮЪЙгУ![]() ЩЈТыгУГЕКѓЃЌЖМПЩЛёЕУвЛеХЦяааШЏЃЌгУЛЇЦяаавЛ-ДЮЛёЕУ
ЩЈТыгУГЕКѓЃЌЖМПЩЛёЕУвЛеХЦяааШЏЃЌгУЛЇЦяаавЛ-ДЮЛёЕУ![]() дЊШЏЃЌЛёЕУ
дЊШЏЃЌЛёЕУ![]() дЊШЏЕФИХТЪЗжБ№ЪЧ
дЊШЏЕФИХТЪЗжБ№ЪЧ![]() ЃЌЧвИїДЮЛёШЁЦяааШЏЕФНсЙћЯрЛЅЖРСЂ.ШєФГгУЛЇвЛЬьЪЙгУСЫСНДЮИУЙЋЫОЕФЙВЯэЕЅГЕЃЌМЧИУгУЛЇЕБЬьЛёЕУЕФЦяааШЏУцЖюжЎКЭЮЊ
ЃЌЧвИїДЮЛёШЁЦяааШЏЕФНсЙћЯрЛЅЖРСЂ.ШєФГгУЛЇвЛЬьЪЙгУСЫСНДЮИУЙЋЫОЕФЙВЯэЕЅГЕЃЌМЧИУгУЛЇЕБЬьЛёЕУЕФЦяааШЏУцЖюжЎКЭЮЊ![]() ЃЌЧѓЫцЛњБфСП
ЃЌЧѓЫцЛњБфСП![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ИН:ЯТБпЕФСйНчжЕБэНіЙЉВЮПМ:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ВЮПМЙЋЪН: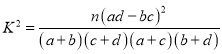 ЃЌЦфжа
ЃЌЦфжа![]() )
)
ЁОД№АИЁПЃЈ1ЃЉдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТЃЌВЛФмШЯЮЊгХЛнЛюЖЏКУЦРгыГЕСОзДПіКУЦРгаЙиЯЕЃЛЃЈ2ЃЉЯъМћНтЮі.
ЕФЧАЬсЯТЃЌВЛФмШЯЮЊгХЛнЛюЖЏКУЦРгыГЕСОзДПіКУЦРгаЙиЯЕЃЛЃЈ2ЃЉЯъМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉга![]() СаСЊБэЕФЪ§ОнЧѓГі
СаСЊБэЕФЪ§ОнЧѓГі![]() ЃЌДгЖјдкЗИДэЮѓЕФИХТЪВЛГЌЙ§
ЃЌДгЖјдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТЃЌВЛФмШЯЮЊгХЛнЛюЖЏКУЦРгыГЕСОзДПіКУЦРгаЙиЯЕЃЛ
ЕФЧАЬсЯТЃЌВЛФмШЯЮЊгХЛнЛюЖЏКУЦРгыГЕСОзДПіКУЦРгаЙиЯЕЃЛ
ЃЈ2ЃЉгЩЬтвтЃЌПЩжЊвЛДЮЦяаагУЛЇЛёЕУ![]() дЊЕФИХТЪЮЊ
дЊЕФИХТЪЮЊ![]() ЃЌ
ЃЌ![]() ЕФЫљгаПЩФмШЁжЕЮЊ
ЕФЫљгаПЩФмШЁжЕЮЊ![]() ЃЌЗжБ№ФмЧѓГі
ЃЌЗжБ№ФмЧѓГі![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЃЈ1ЃЉгЩ![]() СаСЊБэЕФЪ§ОнЃЌга
СаСЊБэЕФЪ§ОнЃЌга
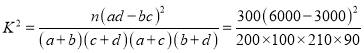
![]()
вђДЫЃЌдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТЃЌВЛФмШЯЮЊгХЛнЛюЖЏКУЦРгыГЕСОзДПіКУЦРгаЙиЯЕЃЛ
ЕФЧАЬсЯТЃЌВЛФмШЯЮЊгХЛнЛюЖЏКУЦРгыГЕСОзДПіКУЦРгаЙиЯЕЃЛ
ЃЈ2ЃЉгЩЬтвтЃЌПЩжЊвЛДЮЦяаагУЛЇЛёЕУ![]() дЊЕФИХТЪЮЊ
дЊЕФИХТЪЮЊ![]() ЃЌ
ЃЌ
![]() ЕФЫљгаПЩФмШЁжЕЮЊ
ЕФЫљгаПЩФмШЁжЕЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ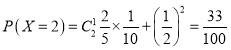
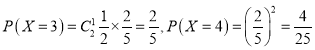
![]() ЕФЗжВМСаЮЊ:
ЕФЗжВМСаЮЊ:
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() ЕФЪ§бЇЦкЭћЮЊ
ЕФЪ§бЇЦкЭћЮЊ![]() .
.