题目内容
7.(理科)已知f(x)=$\frac{a}{{a}^{2}-1}$(ax-a-x) (a>0且a≠1).(1)判断f(x)的奇偶性.
(2)讨论f(x)单调性.
分析 (1)定义域容易得到为R,然后可求出f(-x)=-f(x),从而得出f(x)为奇函数;
(2)根据单调性的定义,设任意的x1<x2,然后作差,通分,提取公因式便可得到$f({x}_{1})-f({x}_{2})=\frac{a}{{a}^{2}-1}$$({a}^{{x}_{1}}-{a}^{{x}_{2}})(1+\frac{1}{{a}^{{x}_{1}}{a}^{{x}_{2}}})$,讨论a>1和0<a<1,从而判断出$\frac{a}{{a}^{2}-1}$的符号,根据指数函数的单调性从而判断出${a}^{{x}_{1}}-{a}^{{x}_{2}}$的符号,从而得出f(x1)与f(x2)的大小关系,这便可得出f(x)的单调性.
解答 解:(1)f(x)定义域为R,f(-x)=$\frac{a}{{a}^{2}-1}({a}^{-x}-{a}^{x})=-f(x)$;
∴f(x)为奇函数;
(2)设x1,x2∈R,且x1<x2,则:
$f({x}_{1})-f({x}_{2})=\frac{a}{{a}^{2}-1}({a}^{{x}_{1}}-{a}^{-{x}_{1}}-{a}^{{x}_{2}}+{a}^{-{x}_{2}})$=$\frac{a}{{a}^{2}-1}({a}^{{x}_{1}}-{a}^{{x}_{2}})(1+\frac{1}{{a}^{{x}_{1}}{a}^{{x}_{2}}})$;
∵a>0且a≠1;
∴①a>1时,$\frac{a}{{a}^{2}-1}>0$;
∵x1<x2;
∴${a}^{{x}_{1}}<{a}^{{x}_{2}},{a}^{{x}_{1}}-{a}^{{x}_{2}}<0$,$1+\frac{1}{{a}^{{x}_{1}}{a}^{{x}_{2}}}>0$;
∴f(x1)-f(x2)<0;
∴f(x1)<f(x2);
∴f(x)在R上为增函数;
②0<a<1时,$\frac{a}{{a}^{2}-1}<0$;
∵x1<x2;
∴${a}^{{x}_{1}}-{a}^{{x}_{2}}>0$;
∴f(x1)<f(x2);
∴f(x)在R为增函数;
∴对任意的a>0,且a≠1,f(x)在R上为增函数.
点评 考查函数奇偶性的定义,及判断函数奇偶性的方法和过程,函数单调性的定义,以及根据函数单调性定义判断一个函数单调性的方法和过程,作差的方法比较f(x1),f(x2),作差后,是分式的一般要通分,一般要提取公因式.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案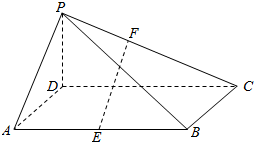 在如图所示的四棱锥中,底面ABCD是平行四边形,AB=4,BC=2,∠BCD=60°,且PD⊥底面ABCD,点E是AB的中点,点F是PC上一点.
在如图所示的四棱锥中,底面ABCD是平行四边形,AB=4,BC=2,∠BCD=60°,且PD⊥底面ABCD,点E是AB的中点,点F是PC上一点.