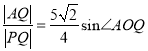题目内容
【题目】已知函数
，
．
（1）若
存在极大值
，证明：
；
（2）若关于
的不等式
在区间
上恒成立，求
的取值范围．
【答案】（1）证明见解析；（2）
．
【解析】
（1）
．（x∈（0，+∞））．对a分类讨论，即可得出单调性极值．进而证明结论．
（2）令h（x）=f（x）+ex-1-1=lnx-ax+a+ex-1-1，x∈[1，+∞），h（1）=0．
，
，对a分类讨论，利用导数研究函数的单调性、极值与最值即可得出．
（1）
当
时，
，
单调递增，不存在极大值，
所以
，在
上单调递增，在
上单调递减，
的极大值为
．
设
，
，
在
上单调递减，在
上单调递增，
．
所以的极大值大于等于0．
（2）设
，
，，
所以
单调递增，
由
知
在上单调递减，在上单调递增，
，
，
若
，则
，
在
恒成立，
此时，函数
在上单调递增，
，满足条件．
若
，则
，所以存在
使得
，
即在
内，有
，在上单调递减，
不满足条件．
综上，
．
练习册系列答案
相关题目
【题目】某农科站技术员为了解某品种树苗的生长情况，在该批树苗中随机抽取一个容量为100的样本，测量树苗高度（单位：
）．经统计，高度在区间
内，将其按
，
，
，
，
，
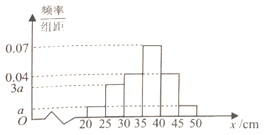
分成6组，制成如图所示的频率分布直方图，其中高度不低于
的树苗为优质树苗．
附：
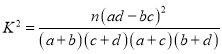，其中
|
|
|
|
|
|
|
|
|
|
（1）求频率分布直方图中
的值；
（2）已知所抽取的这100棵树苗来自于甲、乙两个地区，部分数据如下
列联表所示，将列联表补充完整，并根据列联表判断是否有
％的把握认为优质树苗与地区有关？
甲地区 | 乙地区 | 合计 | |
优质树苗 | 5 | ||
非优质树苗 | 25 | ||
合计 |
