题目内容
3.若关于x的方程$\sqrt{1-{x}^{2}}$=lg(x-a)有正数解,则实数a的取值范围( )| A. | -10<a≤0 | B. | -1<a≤0 | C. | 0≤a<1 | D. | 0≤a<10 |
分析 根据函数和方程之间的关系,将方程转化为两个函数的交点问题,利用数形结合进行求解即可.
解答 解:令f(x)=$\sqrt{1-{x}^{2}}$,g(x)=lg(x-a),
则f(x)的轨迹为半径为1的上半圆,
作出两个函数的图象如图;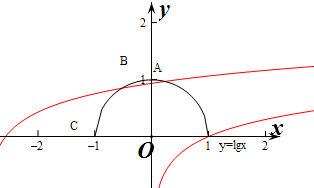
当a=0时,g(x)=lgx,过(1,0)点,满足条件,
当a≠0时,
若关于x的方程$\sqrt{1-{x}^{2}}$=lg(x-a)有正数解,
则满足g(1)≥0且g(0)<1,
即$\left\{\begin{array}{l}{lg(1-a)≥0}\\{lg(-a)<1}\end{array}\right.$,
即$\left\{\begin{array}{l}{1-a≥1}\\{0<-a<10}\end{array}\right.$,
则$\left\{\begin{array}{l}{a≤0}\\{-10<a<0}\end{array}\right.$,交点-10<a<0,
综上-10<a≤0,
故实数a的取值范围是(-10,0],
故选:A
点评 本题主要考查方程根的个数的应用,根据函数和方程之间的关系转化为两个函数的交点问题是解决本题的关键.

练习册系列答案
相关题目
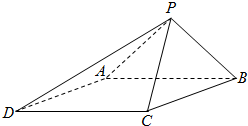 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.