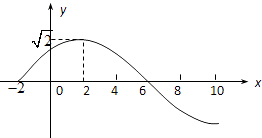题目内容
【题目】给出下列命题:
①在△ABC中,若A<B,则sinA<sinB;
②在同一坐标系中,函数y=sinx与y=lgx的交点个数为2个;
③函数y=|tan2x|的最小正周期为 ![]() ;
;
④存在实数x,使2sin(2x﹣ ![]() )﹣1=
)﹣1= ![]() 成立;
成立;
其中正确的命题为(写出所有正确命题的序号).
【答案】①③
【解析】解:①在△ABC中,若A<B,由正弦定理得a<b,则由 ![]() 得sinA<sinB成立,故①正确;
得sinA<sinB成立,故①正确;
②在同一坐标系中,作出函数y=sinx与y=lgx图象如图:
∵lg10=1,∴两个图象的交点个数为3个;故②错误,
③函数y=|tan2x|的最小正周期和y=tan2x的周期相同,为T= ![]() ,故③正确,;
,故③正确,;
④由2sin(2x﹣ ![]() )﹣1=
)﹣1= ![]() ,得sin(2x﹣
,得sin(2x﹣ ![]() )=
)= ![]() >1,
>1,
则不存在实数x,使2sin(2x﹣ ![]() )﹣1=
)﹣1= ![]() 成立;故④错误,
成立;故④错误,
所以答案是:①③
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目