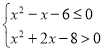题目内容
【题目】在数列![]() 中,若
中,若![]() 且
且 则称
则称![]() 为“
为“![]() 数列”.设
数列”.设![]() 为“
为“![]() 数列”,记
数列”,记![]() 的前
的前![]() 项和为
项和为![]()
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)证明:![]() 中总有一项为
中总有一项为![]() 或
或![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据递推公式列出数列![]() 中的项,找规律,发现周期性即可得到答案;
中的项,找规律,发现周期性即可得到答案;
(2)根据题意分情况进行求解即可得到答案;
(3)首先证明:一定存在某个![]() ,使得
,使得![]() 成立,再进行检验即可得到答案.
成立,再进行检验即可得到答案.
(1)当![]() 时,
时,![]() 中的各项依次为
中的各项依次为![]() ,
,
即数列![]() 从第四项开始每三项是一个周期,
从第四项开始每三项是一个周期,
所以![]() ,
,![]() ,
,
![]() ,
,
所以![]() .
.
(2)① 若![]() 是奇数,则
是奇数,则![]() 是偶数,
是偶数,![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() ,适合题意.
,适合题意.
② 若![]() 是偶数,不妨设
是偶数,不妨设![]() ,则
,则![]() .
.
若![]() 是偶数,则
是偶数,则![]() ,由
,由![]() ,
,
得![]() ,此方程无整数解;
,此方程无整数解;
若![]() 是奇数,则
是奇数,则![]() ,由
,由![]() ,
,
得![]() ,此方程无整数解.
,此方程无整数解.
综上,![]() .
.
(3)首先证明:一定存在某个![]() ,使得
,使得![]() 成立.
成立.
否则,对每一个![]() ,都有
,都有![]() ,
,
则在![]() 为奇数时,必有
为奇数时,必有![]() ;
;
在![]() 为偶数时,有
为偶数时,有![]() ,或
,或![]() .
.
因此,若对每一个![]() ,都有
,都有![]() ,则
,则![]() 单调递减,
单调递减,
注意到![]() ,显然这一过程不可能无限进行下去,
,显然这一过程不可能无限进行下去,
所以必定存在某个![]() ,使得
,使得![]() 成立.
成立.
经检验,当![]() ,或
,或![]() ,或
,或![]() 时,
时,![]() 中出现
中出现![]() ;
;
当![]() 时,
时,![]() 中出现
中出现![]() ,
,
综上,![]() 中总有一项为
中总有一项为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某农科所为改良玉米品种,对已选出的一组玉米的茎高进行统计,获得茎叶图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
抗倒伏 | 易倒伏 | 总计 | |
矮茎 | |||
高茎 | |||
总计 |
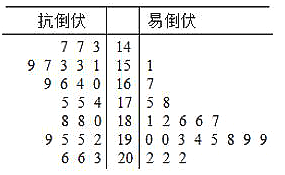
(1)请完成以上![]() 列联表,并判断是否可以在犯错误的概率不超过0.01的前提下,认为抗倒伏与玉米矮茎有关?
列联表,并判断是否可以在犯错误的概率不超过0.01的前提下,认为抗倒伏与玉米矮茎有关?
(2)为改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,则选取的植株均为矮茎的概率是多少?
参考公式: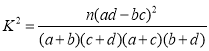 (其中
(其中![]() )
)
参考数据:
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |