题目内容
【题目】△ABC中，a、b、c分别是角A、B、C的对边，向量
＝(2sinB,2－cos2B)，
＝(2sin2(
)，－1)，
.
(1)求角B的大小；
(2)若a＝
，b＝1，求c的值．
【答案】（1）
或
； （2）c＝2或c＝1.
【解析】
(1)根据
＝0得到4sinB·sin2
＋cos2B－2＝0，再化简即得B＝ 或 .(2)先确定B的值，再利用余弦定理求出c的值.
(1)∵
，∴＝0，∴4sinB·sin2＋cos2B－2＝0，
∴2sinB[1－cos
]＋cos2B－2＝0，∴2sinB＋2sin2B＋1－2sin2B－2＝0，
∴sinB＝
，∵0<B<π，∴B＝ 或 .
(2)∵a＝
，b＝1，∴a>b，∴此时B＝，
由余弦定理得：b2＝a2＋c2－2accosB，∴c2－3c＋2＝0，∴c＝2或c＝1.
综上c＝2或c＝1.
练习册系列答案
相关题目
【题目】某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率，选取
名工人，将他们随机分成两组，每组
人.第一组工人用第一种生产方式，第二组工人用第二种生产方式.根据工人完成生产任务的工作时间（单位：
）绘制了如图所示的茎叶图（茎为十位数，叶为个位数）：
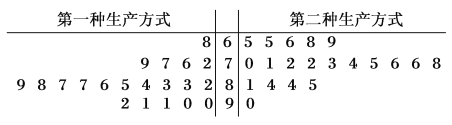
（1）根据茎叶图，估计两种生产方式完成任务所需时间至少
分钟的概率，并对比两种生产方式所求概率，判断哪种生产方式的效率更高？
（2）将完成生产任务所需时间超过和不超过的工人数填入下面的列联表：
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
（3）根据（2）中的列联表，能否有
的把握认为两种生产方式的效率有差异？
附：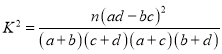
|
|
|
|
|
|
|
|
