��Ŀ����
6����֪��ԲC��$\frac{{x}^{2}}{{b}^{2}}$+$\frac{{y}^{2}}{{a}^{2}}$=1��a��b��0����������e=$\frac{{\sqrt{2}}}{2}$���Ҷ���ΪA����M��1��0��Ϊ�߶�OA���е㣬����OΪ����ԭ�㣮��������ԲC�ķ��̣�
������M����һ��ֱ�߽���ԲC�ڲ�ͬ������E��F��������x�����Ƿ���ڶ���N��ʹ�á�ENM=��FNM�������ڣ������N�����ꣻ�������ڣ�˵�����ɣ�
���� ����ͨ����M��1��0��Ϊ�߶�OA���е��֪b=2������$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$��a2-b2=c2�����㼴�ý��ۣ�
���� ͨ������ڵ�N��x0��0������������������EF��x���ֱ�벻��ֱ����������ۣ�����Τ�ﶨ�������㼴�ý��ۣ�
��� �⣺���� ������ɵ�b=2��
����Ϊ$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$��a2-b2=c2��
���� $a=2\sqrt{2}$��
��������ԲC�ķ���Ϊ$\frac{x^2}{4}+\frac{y^2}{8}=1$��
���� ���ۣ���x���ϴ��ڵ�N��4��0����ʹ�á�ENM=��FNM��
�������£�
������ڵ�N��x0��0����������������
��1����EF��x���ֱʱ����EF�ķ���Ϊy=k��x-1����
��$\left\{\begin{array}{l}y=k��x-1��\\ \frac{x^2}{4}+\frac{y^2}{8}=1\end{array}\right.$��ȥy�������ã���2+k2��x2-2k2x+k2-8=0��
��֪����0����E��x1��y1����F��x2��y2����
��${x_1}+{x_2}=\frac{{2{k^2}}}{{2+{k^2}}}$��${x_1}{x_2}=\frac{{{k^2}-8}}{{2+{k^2}}}$��
${k_{EN}}+{k_{FN}}=\frac{y_1}{{{x_1}-{x_0}}}+\frac{y_2}{{{x_2}-{x_0}}}=\frac{{k��{x_1}-1��}}{{{x_1}-{x_0}}}+\frac{{k��{x_2}-1��}}{{{x_2}-{x_0}}}$=$\frac{{k��{x_1}-1����{x_2}-{x_0}��+k��{x_2}-1����{x_1}-{x_0}��}}{{��{x_1}-{x_0}����{x_2}-{x_0}��}}$��
��x1-1����x2-x0��+��x2-1����x1-x0��=2x1x2-��1+x0����x1+x2��+2x0=$\frac{2��{k}^{2}-8��}{2+{k}^{2}}$-$\frac{2��1+{x}_{0}��{k}^{2}}{2+{k}^{2}}$+2x0��
����ENM=��FNM����kEN+kFN=0��$��\;k[{\frac{{2��{k^2}-8��}}{{2+{k^2}}}-\frac{{2��1+{x_0}��{k^2}}}{{2+{k^2}}}+2{x_0}}]=0$��
�����ã�k��x0-4��=0����Ϊk��R������x0=4��
��2����EF��x��ʱ������Բ�ĶԳ��Կ�֪���С�ENM=��FNM���������⣻
���ϣ���x���ϴ��ڵ�N��4��0����ʹ�á�ENM=��FNM��
���� ���⿼����Բ�ļ����ʣ�ע����ⷽ���Ļ��ۣ������е��⣮

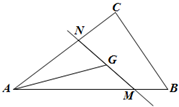 ��ͼ��ֱ��MN����ABC������G���������������������ߵĽ��㣩����$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AC}$=$\overrightarrow{b}$����$\overrightarrow{AM}$=m$\overrightarrow{a}$��$\overrightarrow{AN}$=n$\overrightarrow{b}$������m��0��n��0������mn����Сֵ�ǣ�������
��ͼ��ֱ��MN����ABC������G���������������������ߵĽ��㣩����$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AC}$=$\overrightarrow{b}$����$\overrightarrow{AM}$=m$\overrightarrow{a}$��$\overrightarrow{AN}$=n$\overrightarrow{b}$������m��0��n��0������mn����Сֵ�ǣ�������| A�� | $\frac{2}{9}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{4}{9}$ | D�� | $\frac{2}{3}$ |
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
| A�� | ��1��$\sqrt{3}$�� | B�� | ��$\sqrt{3}$��2�� | C�� | ��2��+�ޣ� | D�� | ��1��2�� |
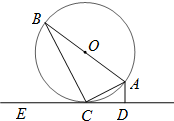 ��ͼ��ԲO��AB=4Ϊֱ����ֱ��CE��ԲO�����ڵ�C��AD��CE�ڵ�D����AD=1����ACD=�ȣ���cos��=$\frac{\sqrt{3}}{2}$��
��ͼ��ԲO��AB=4Ϊֱ����ֱ��CE��ԲO�����ڵ�C��AD��CE�ڵ�D����AD=1����ACD=�ȣ���cos��=$\frac{\sqrt{3}}{2}$��