题目内容
【题目】设函数f（x）= 
，若f（﹣4）=f（0），f（﹣2）=﹣1．
（1）求函数f（x）的解析式；
（2）画出函数f（x）的图象，并指出函数的定义域、值域、单调区间． 
【答案】
（1）解：由f（﹣4）=f（0），f（﹣2）=﹣1，
即有16﹣4b+c=3，4﹣2b+c=﹣1，
解得：b=4，c=3，
则f（x）= 
（2）解：图象见图所示：
由图象可知：函数的定义域：[﹣4，+∞）；
值域：（﹣∞，3]；
单调增区间：（﹣2，0），单调减区间：（﹣4，﹣2），（0，+∞）．
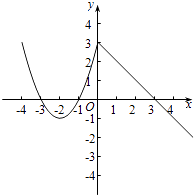
【解析】（1）由题意可得16﹣4b+c=3，4﹣2b+c=﹣1，解方程可得b，c，进而得到f（x）的解析式；（2）由分段函数的画法，可得f（x）的图象，进而得到定义域、值域、单调区间．
练习册系列答案
相关题目
