题目内容
设f(x)是定义在R上的奇函数,且对任意实数x恒满足f(x+2)=-f(x),当x∈[0,2]时,f(x)=2x-x2.
(1)求证:f(x)是周期函数.
(2)当x∈[2,4]时,求f(x)的解析式.
(3)计算f(0)+f(1)+f(2)+…+f(2011)
(1)求证:f(x)是周期函数.
(2)当x∈[2,4]时,求f(x)的解析式.
(3)计算f(0)+f(1)+f(2)+…+f(2011)
(1)∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
∴f(x)是周期为4的周期函数.
(2)当x∈[-2,0]时,-x∈[0,2],由已知
f(-x)=2(-x)-(-x)2=-2x-x2,
又f(x)为奇函数,∴-f(x)=-2x-x2.
∴f(x)=x2+2x.当x∈[2,4]时,x-4∈[-2,0].
∴f(x-4)=(x-4)2+2(x-4),
又f(x)是周期为4的周期函数,
∴f(x)=f(x-4)=(x-4)2+2(x-4)=x2-6x+8,
∴x∈[2,4]时,f(x)=x2-6x+8.
(3)∵f(0)=0,f(1)=1,f(2)=0,f(3)=-1.
又f(x)是周期为4的周期函数.
∴f(0)+f(1)+f(2)+f(3)=f(4)+f(5)+f(6)+f(7)
=…=f(2004)+f(2005)+f(2006)+f(2007)
=f(2010)+f(2009)+f(2010)+f(2011)=0.
∴f(0)+f(1)+…+f(2011)=0+…+0=0.
∴f(x+4)=-f(x+2)=f(x),
∴f(x)是周期为4的周期函数.
(2)当x∈[-2,0]时,-x∈[0,2],由已知
f(-x)=2(-x)-(-x)2=-2x-x2,
又f(x)为奇函数,∴-f(x)=-2x-x2.
∴f(x)=x2+2x.当x∈[2,4]时,x-4∈[-2,0].
∴f(x-4)=(x-4)2+2(x-4),
又f(x)是周期为4的周期函数,
∴f(x)=f(x-4)=(x-4)2+2(x-4)=x2-6x+8,
∴x∈[2,4]时,f(x)=x2-6x+8.
(3)∵f(0)=0,f(1)=1,f(2)=0,f(3)=-1.
又f(x)是周期为4的周期函数.
∴f(0)+f(1)+f(2)+f(3)=f(4)+f(5)+f(6)+f(7)
=…=f(2004)+f(2005)+f(2006)+f(2007)
=f(2010)+f(2009)+f(2010)+f(2011)=0.
∴f(0)+f(1)+…+f(2011)=0+…+0=0.
略

练习册系列答案
相关题目
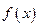 是定义在R上的奇函数,若
是定义在R上的奇函数,若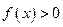 。则以下不等式不一定成立的是 ( )
。则以下不等式不一定成立的是 ( )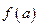 >
>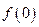
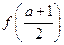 >
>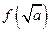
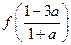 >
>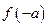
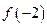
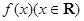 为奇函数,
为奇函数,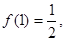
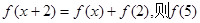 = ( )
= ( )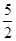
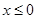 时
时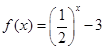 ,则
,则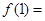 ( )
( )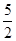
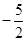
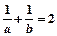 ,则A=____
,则A=____ ____。
____。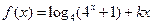
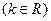 是偶函数,则
是偶函数,则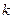 的值为
的值为 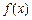 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当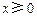 时,
时,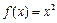 ,若对任意的
,若对任意的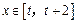 ,不等式
,不等式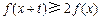 恒成立,则实数
恒成立,则实数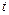 的取值范围是 .
的取值范围是 .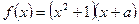 为奇函数,则
为奇函数,则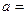 ______.
______.