题目内容
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" =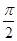 ,AB=BC=2AD=4,
,AB=BC=2AD=4,
E、F分别是AB、CD上的点,且EF∥BC.设AE =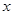 ,G是BC的中点.
,G是BC的中点.
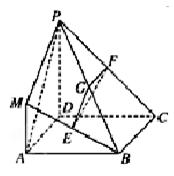
沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(1)当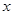 =2时,求证:BD⊥EG ;
=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
(3)当 取得最大值时,求二面角D-BF-E的余弦值.
取得最大值时,求二面角D-BF-E的余弦值.
(1)见解析;(2)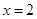 时
时 有最大值为
有最大值为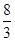 .(3)cos<
.(3)cos< >=
>=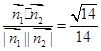 。
。
解析试题分析:(1)∵平面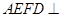 平面
平面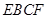 ,
,
 AE⊥EF,∴AE⊥平面
AE⊥EF,∴AE⊥平面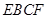 ,AE⊥EF,AE⊥BE,又BE⊥EF,
,AE⊥EF,AE⊥BE,又BE⊥EF,
据此建立建立空间坐标系E-xyz.然后利用 ,证得
,证得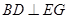 .
.
(2)∵AD∥面BFC,利用  建立关于x的一元二次函数,求出其最大值.
建立关于x的一元二次函数,求出其最大值.
(3)在(2)的条件下,分别求出二面角D-BF-E两个面的法向量,根据法向量的夹角与二面角相等或互补求解.
(1)方法一:
∵平面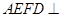 平面
平面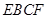 ,
,
 AE⊥EF,∴AE⊥平面
AE⊥EF,∴AE⊥平面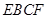 ,AE⊥EF,AE⊥BE,
,AE⊥EF,AE⊥BE,
又BE⊥EF,故可如图建立空间坐标系E-xyz.
 ,又
,又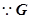 为BC的中点,BC=4,
为BC的中点,BC=4,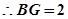 .则A(0,0,2),B(2,0,0),
.则A(0,0,2),B(2,0,0),
G(2,2,0),D(0,2,2),E(0,0,0),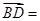 (-2,2,2),
(-2,2,2),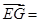 (2,2,0),
(2,2,0),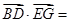 (-2,2,2)
(-2,2,2)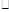 (2,2,0)=0,
(2,2,0)=0,
∴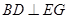 .……4分
.……4分
方法二:
作DH⊥EF于H,连BH,GH, 由平面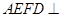 平面
平面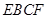 知:DH⊥平面EBCF,
知:DH⊥平面EBCF,
而EG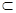 平面EBCF,故EG⊥DH.
平面EBCF,故EG⊥DH. 为平行四边形,
为平行四边形, 且
且 ,
, 四边形BGHE为正方形,∴EG⊥BH,BH
四边形BGHE为正方形,∴EG⊥BH,BH DH=H,
DH=H,
故EG⊥平面DBH, 而BD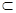 平面DBH,∴ EG⊥BD.………4分
平面DBH,∴ EG⊥BD.………4分
(或者直接利用三垂线定理得出结果)
(2)∵AD∥面BFC,所以 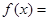
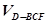 =VA-BFC=
=VA-BFC=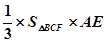
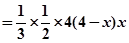
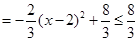 ,即
,即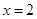 时
时 有最大值为
有最大值为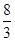 . ………8分
. ………8分
(3)设平面DBF的法向量为 ,∵AE=2, B(2,0,0),
,∵AE=2, B(2,0,0),
D(0,2,2),F(0,3,0),∴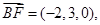 ………9分
………9分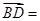 (-2,2,2),
(-2,2,2),
则  ,即
,即 ,
,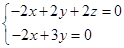
取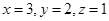 ,∴
,∴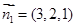
 ,
, 面BCF一个法向量为
面BCF一个法向量为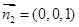 ,
,
则cos< >=
>=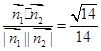 ,………14分.
,………14分.
考点:空间向量法在证明与求角当中的应用.
点评:利用空间向量法关键是选择恰当的坐标系,本小题在证明AE⊥EF,AE⊥BE,
BE⊥EF的基础上,可如图建立空间坐标系E-xyz.下面利用两向量数量积为零来证明直线垂直,求两个面的法向量的夹角来求二面角即可.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
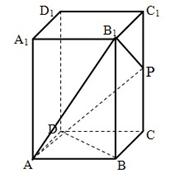
宝贝计划期末冲刺夺100分系列答案 的正方体
的正方体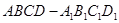 中分离出来的:
中分离出来的: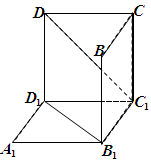
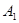 是否在平面
是否在平面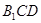 内;(回答是与否)
内;(回答是与否)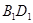 与
与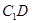 所成的角;
所成的角;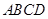 中,
中, 为正三角形,
为正三角形,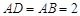 ,
,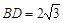 ,
,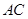 与
与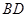 交于
交于 点.将
点.将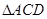 沿边
沿边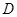 点至
点至 点,已知
点,已知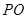 与平面
与平面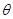 ,且
,且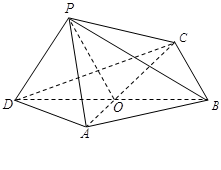
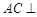 平面
平面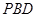 ;
;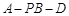 的余弦值为
的余弦值为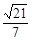 ,求
,求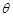 的大小.
的大小.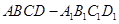 中,
中,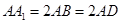 ,且
,且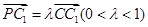 .
.
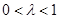 ,总有
,总有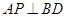 ;
;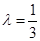 ,求二面角
,求二面角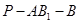 的余弦值;
的余弦值;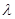 ,使得
,使得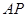 在平面
在平面 上的射影平分
上的射影平分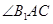 ?若存在, 求出
?若存在, 求出 的底面为直角梯形,
的底面为直角梯形,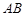 //
//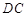 ,
,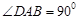 ,
,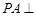 底面
底面 ,且
,且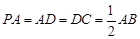 .
.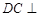 平面
平面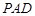 ;
; 的余弦值的大小.
的余弦值的大小.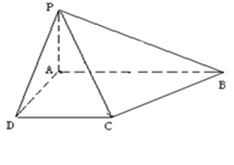
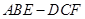 的三视图如图,
的三视图如图,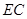 与
与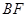 交于点
交于点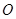 ,
,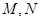 分别是直线
分别是直线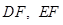 的中点,
的中点, 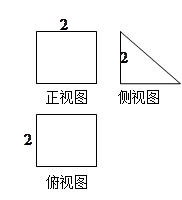
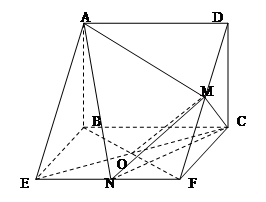
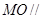 面
面 ;
;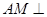 面
面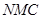 ;
;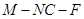 的平面角的余弦值.
的平面角的余弦值.